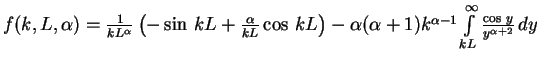- ...
known1.1
- At zero temperature the expectation value
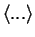 is
taken with respect to the ground state of the system.
is
taken with respect to the ground state of the system.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrix1.2
- It is
interesting to note that the normalization factor
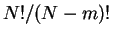 of the
of the 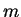 -body
correlation function comes from the number of ways to make groups of
-body
correlation function comes from the number of ways to make groups of 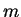 -particles
out of
-particles
out of 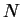 particles, but at the same time can be found from the properties of the
field operators
particles, but at the same time can be found from the properties of the
field operators
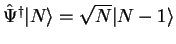 ,
,
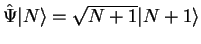
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
wave1.3
- The normalization of the scattering solution is of no interest to us,
so in following we will always omit the normalization factor.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sphere1.4
- Note that
therefore the energy is purely kinetic and the interaction potential does not enter
in an explicit way, instead it sets the boundary condition on the solution.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... as1.5
- In the three-dimensional system we
look for solutions with spherical symmetry. In a one-dimensional system it is
equivalent to searching even solutions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scattering1.6
- The textbook definition
for the three-dimensional scattering length (1.44) can be recasted in a similar
form
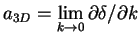 . We prefer to have a
definition in terms of a derivative, as it does not cause any ambiguity in the
choice a free particle phase. In three dimensions the phase of sinus (1.42) in
absence of the scattering potential is fixed to zero due to the condition
(1.40), which is no longer so in
. We prefer to have a
definition in terms of a derivative, as it does not cause any ambiguity in the
choice a free particle phase. In three dimensions the phase of sinus (1.42) in
absence of the scattering potential is fixed to zero due to the condition
(1.40), which is no longer so in 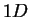 case, as it should be fixed to
case, as it should be fixed to 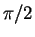 .
Instead the definition (1.63) takes into account the difference between the
phase in presence of scatterer and in its absence. See also footnote
on p.
.
Instead the definition (1.63) takes into account the difference between the
phase in presence of scatterer and in its absence. See also footnote
on p. ![[*]](http://www.science.unitn.it/~astra/PhD/icons/crossref.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... solution1.7
- It turns out that this property is general and can be
used as an alternative to (1.63) definition of the one-dimensional
scattering length.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
obtain1.8
- We used property
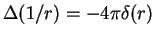 , which can be
easily obtained from the solution
, which can be
easily obtained from the solution
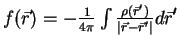 to the Poisson equation
to the Poisson equation
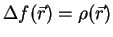 substituting the point charge
substituting the point charge
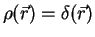 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... equation1.9
- Additional
literature on the topic of pseudopotential description can be found in classical
articles [Fer36],[HY57] and in books [BW52],p.74,
[Hua87].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
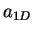 1.10
1.10
- As discussed
in Sec. 1.3.3.4, the size of a hard-rod equals to the one-dimensional scattering
length on HR potential (1.79).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
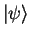 1.11
1.11
- It is important to
note that
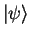 is not a wave function and in this sense the derived below
GPE (1.115) is not a ``non linear Schrödinger equation''. In particular its
time evolution is driven by the chemical potential
is not a wave function and in this sense the derived below
GPE (1.115) is not a ``non linear Schrödinger equation''. In particular its
time evolution is driven by the chemical potential 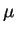 instead of the energy of
the system
instead of the energy of
the system 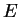 , as it happens for the solution of the Schrödinger equation.
, as it happens for the solution of the Schrödinger equation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... has1.12
- This approximation is called polytropic.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1.121.13
- Many
theories produces results that fall into the class of equations of state described
by formula (1.136). For example GP theory, ideal fermi gas, TG gas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is1.14
- S. Stringari,
unpublished.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... LDA1.15
- It
is interesting to note that the result (1.151) of an approximate
solution for particles of infinite repulsion coincides with an exact result
for particles interacting with
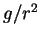 interaction (Calogero-Sutherland model
[Cal69,Sut71]) in the limit
interaction (Calogero-Sutherland model
[Cal69,Sut71]) in the limit 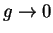 . Indeed, as shown in
[Sut71] the energy of such a gas equals
. Indeed, as shown in
[Sut71] the energy of such a gas equals
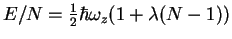 , where
, where 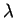 is related to the
strength of interaction
is related to the
strength of interaction
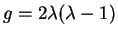 . There are two different ways of
taking the limit
. There are two different ways of
taking the limit 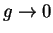 : 1)
: 1) 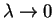 ,
,
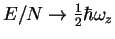 i.e.
this limit corresponds to non-interacting bosons all staying in the lowest state of
a harmonic oscillator 2)
i.e.
this limit corresponds to non-interacting bosons all staying in the lowest state of
a harmonic oscillator 2) 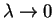 ,
,
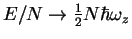 , i.e.
this limit preserves the singularity of the interaction while makes the potential
energy vanishing.
, i.e.
this limit preserves the singularity of the interaction while makes the potential
energy vanishing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... density1.16
- In this section we keep a different notation
for the linear density
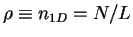
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...exact2.1
- Of course, as this method is a
statistical one and all outputs are obtained within statistical errors which can be
decreased by making a longer series of measurements.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... as2.2
- The
subscript
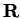 of the differential operator indicates that the derivative
has to be taken for every component of
of the differential operator indicates that the derivative
has to be taken for every component of 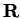 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function2.3
- for details of the
calculation refer to Sec. 2.7
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
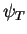 2.4
2.4
- The definition (2.15) of the drift force can be
understood in a classical analogy. In a classical system the probability
distribution has a Boltzman form. The coordinate part of the distribution function
is related to the potential energy
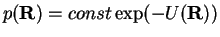 (we put the
fictitious temperature to one). The classical force is an antigradient of the
potential energy
(we put the
fictitious temperature to one). The classical force is an antigradient of the
potential energy
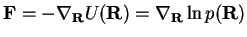 . If we approximate a
quantum probability distribution by the square of a trial wave function (2.1),
then the force equals exactly to (2.15).
. If we approximate a
quantum probability distribution by the square of a trial wave function (2.1),
then the force equals exactly to (2.15).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distribution2.1
- The formula (2.31) should be understood
in the statistical sense, the average of any value
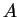 over the l.h.s. and r.h.s
distributions are equal to each other in the limit when size of the population
over the l.h.s. and r.h.s
distributions are equal to each other in the limit when size of the population 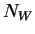 tends to infinity
tends to infinity
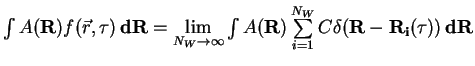
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... as2.2
- Note that for a repulsive gas
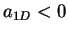 while for attractive
while for attractive 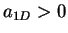 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function3.1
- Mean square radii are calculated using the pure estimator technique developed in [CB95]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... satisfied3.2
- This
characteristic for LDA parameter is universal, for example systems with different
number of particles behave similarly if the combination
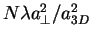 is the same. It becomes clear from
from equation (1.134) noting that
is the same. It becomes clear from
from equation (1.134) noting that
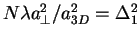 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... by4.1
- See, also,
footnote on p.
![[*]](http://www.science.unitn.it/~astra/PhD/icons/crossref.png)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lengths7.1
- Considering an homogenious condensate, we assume that its
size is large enough, particularly that the gas is the Thomas-Fermi
conditions. Then results for a homogenious gas will be approximately valid for a gas in a trap.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... physics8.1
- See, e.g., [Voi95]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)8.2
- Note that Eqs. 1.69-8.5 are valid
only if the condition
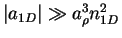 is
satisfied [Ols98].
is
satisfied [Ols98].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
equations8.3
- Details on the numerical solution of the integral equations and a
table for the function
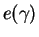 can be downloaded from
http://www.science.unitn.it/~astra/1Dfermions/.
can be downloaded from
http://www.science.unitn.it/~astra/1Dfermions/.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
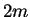 8.4
8.4
- The coefficient and sign of the third term on the right hand
side of Eq. 8.9 differ from Eq. A7 in Ref. [CEE+91].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gas9.1
- Note that for
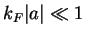 the nonanalytic correction to the ground-state energy due to the
superfluid gap is exponentially small.
the nonanalytic correction to the ground-state energy due to the
superfluid gap is exponentially small.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
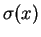 10.1
10.1
-
It is convenient to use following equality
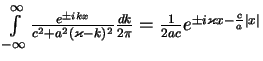
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
analytically11.1
- Compare with [GR80]
![$\int_L^\infty x^{\mu-1} \cos x
dx = \frac{1}{2}[e^{-i\mu\pi/2}\Gamma(\mu, iL)+e^{i\mu\pi/2}\Gamma(\mu, -iL)]$](img1909.gif)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... simplified11.2
- See
[GR80] 3.761.7
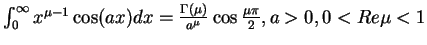
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... obtain11.3
- In dimensionless units
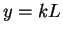 formulae (B.6, B.7) look like
formulae (B.6, B.7) look like
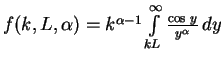 and
and
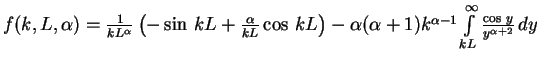
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
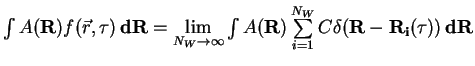
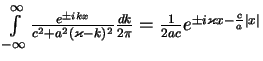
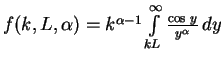 and
and