



Next: Trapped system
Up: Interacting fermions in highly
Previous: Model
Contents
Consider the Hamiltonian 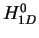 , Eq. 8.3, which describes a
homogeneous 1D two-component Fermi gas. The ground state energy
, Eq. 8.3, which describes a
homogeneous 1D two-component Fermi gas. The ground state energy 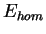 of
of
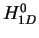 has been calculated exactly using Bethe's ansatz for
attractive [Gau67] and repulsive [Yan67] interactions, and can be
expressed in terms of the linear number density
has been calculated exactly using Bethe's ansatz for
attractive [Gau67] and repulsive [Yan67] interactions, and can be
expressed in terms of the linear number density 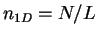 , where
, where 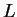 is the size
of the system,
is the size
of the system,
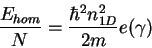 |
(8.6) |
The dimensionless parameter 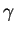 is proportional to the coupling constant
is proportional to the coupling constant
 ,
,
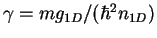 , while its absolute value is inversely
proportional to the 1D gas parameter
, while its absolute value is inversely
proportional to the 1D gas parameter
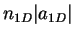 ,
,
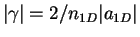 .
The function
.
The function 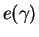 is obtained by solving a set of integral
equations8.3, which is similar to that
derived by Lieb and Liniger [LL63] for 1D bosons with repulsive contact
interactions.
To obtain the energy per particle, Eq. 8.6, we solve these integral
equations for
is obtained by solving a set of integral
equations8.3, which is similar to that
derived by Lieb and Liniger [LL63] for 1D bosons with repulsive contact
interactions.
To obtain the energy per particle, Eq. 8.6, we solve these integral
equations for 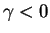 [Gau67] and for
[Gau67] and for 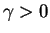 [Yan67].
[Yan67].
Figure 8.2 shows
Figure 8.2:
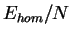 (solid line),
(solid line), 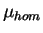 (dashed line)
and
(dashed line)
and 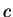 (inset) for a homogeneous two-component 1D Fermi gas as a function of
(inset) for a homogeneous two-component 1D Fermi gas as a function of
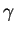 (horizontal arrows indicate the asymptotic values of
(horizontal arrows indicate the asymptotic values of 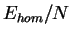 ,
,
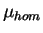 and
and 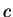 , respectively).
, respectively).
|
|
the energy per particle, 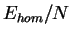 (solid line), the chemical potential
(solid line), the chemical potential
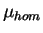 ,
,
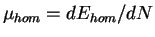 (dashed line), and the velocity of sound
(dashed line), and the velocity of sound 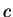 (inset), which is obtained from the inverse compressibility
(inset), which is obtained from the inverse compressibility
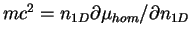 , as a function of the interaction
strength
, as a function of the interaction
strength 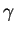 . In the weak coupling limit,
. In the weak coupling limit, 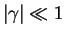 ,
, 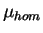 is given
by
is given
by
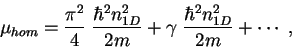 |
(8.7) |
where the first term on the right hand side is the energy of an ideal two-component
atomic Fermi gas, and the second term is the mean-field energy, which accounts for
interactions. The chemical potential increases with increasing 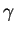 , and reaches
an asymptotic value for
, and reaches
an asymptotic value for
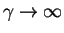 (indicated by a horizontal arrow
in Fig. 8.2),
(indicated by a horizontal arrow
in Fig. 8.2),
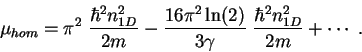 |
(8.8) |
The first term on the right hand side coincides with the chemical potential of a
one-component ideal 1D Fermi gas with 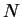 atoms, the second term has been calculated
in [RFZZ03a]. Interestingly, for
atoms, the second term has been calculated
in [RFZZ03a]. Interestingly, for 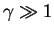 , the strong atom-atom repulsion
between atoms with different spin plays the role of an effective Pauli
principle [RFZZ03a,RFZZ03b].
, the strong atom-atom repulsion
between atoms with different spin plays the role of an effective Pauli
principle [RFZZ03a,RFZZ03b].
For attractive interactions and large enough 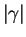 the energy per particle is
negative (see Fig. 8.2), reflecting the existence of a molecular Bose gas,
which consists of
the energy per particle is
negative (see Fig. 8.2), reflecting the existence of a molecular Bose gas,
which consists of 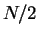 diatomic molecules with binding energy
diatomic molecules with binding energy
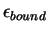 .
Each molecule is comprised of two atoms with different spin. In the limit
.
Each molecule is comprised of two atoms with different spin. In the limit
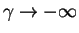 , the chemical potential becomes
, the chemical potential becomes
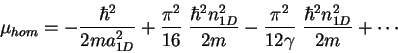 |
(8.9) |
The first term is simply
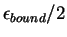 , one half of the binding energy of the
1D molecule, while the second term is equal to half of the chemical potential of a
bosonic Tonks-Girardeau gas with density
, one half of the binding energy of the
1D molecule, while the second term is equal to half of the chemical potential of a
bosonic Tonks-Girardeau gas with density 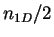 , consisting of
, consisting of 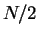 molecules
with mass
molecules
with mass 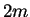 8.4.
Importantly, the compressibility remains positive for
8.4.
Importantly, the compressibility remains positive for
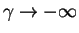 [a horizontal arrow in the inset of Fig. 8.2 indicates the asymptotic
value of
[a horizontal arrow in the inset of Fig. 8.2 indicates the asymptotic
value of 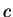 ,
,
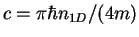 ], which implies that two-component 1D Fermi
gases are mechanically stable even in the strongly-attractive regime. In contrast,
the ground state of 1D Bose gases with
], which implies that two-component 1D Fermi
gases are mechanically stable even in the strongly-attractive regime. In contrast,
the ground state of 1D Bose gases with 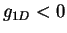 has negative
compressibility [McG64] and is hence mechanically unstable.
has negative
compressibility [McG64] and is hence mechanically unstable.




Next: Trapped system
Up: Interacting fermions in highly
Previous: Model
Contents
G.E. Astrakharchik
15-th of December 2004
![]() , Eq. 8.3, which describes a
homogeneous 1D two-component Fermi gas. The ground state energy
, Eq. 8.3, which describes a
homogeneous 1D two-component Fermi gas. The ground state energy ![]() of
of
![]() has been calculated exactly using Bethe's ansatz for
attractive [Gau67] and repulsive [Yan67] interactions, and can be
expressed in terms of the linear number density
has been calculated exactly using Bethe's ansatz for
attractive [Gau67] and repulsive [Yan67] interactions, and can be
expressed in terms of the linear number density ![]() , where
, where ![]() is the size
of the system,
is the size
of the system,
![\includegraphics[width=7cm]{1DFermiEhom.eps}](1DFermiEhom.gif)
![]() the energy per particle is
negative (see Fig. 8.2), reflecting the existence of a molecular Bose gas,
which consists of
the energy per particle is
negative (see Fig. 8.2), reflecting the existence of a molecular Bose gas,
which consists of ![]() diatomic molecules with binding energy
diatomic molecules with binding energy
![]() .
Each molecule is comprised of two atoms with different spin. In the limit
.
Each molecule is comprised of two atoms with different spin. In the limit
![]() , the chemical potential becomes
, the chemical potential becomes