



Next: Homogeneous system
Up: Interacting fermions in highly
Previous: Introduction
Contents
Consider a two-component atomic Fermi gas confined in a highly-elongated trap. The
fermionic atoms are assumed to belong to the same atomic species, that is, to have
the same mass 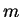 , but to be trapped in different hyperfine states
, but to be trapped in different hyperfine states 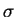 , where
, where
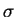 represents a generalized spin or angular momentum,
represents a generalized spin or angular momentum,
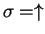 or
or
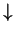 . The trapping potential is assumed to be harmonic and axially
symmetric,
. The trapping potential is assumed to be harmonic and axially
symmetric,
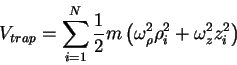 |
(8.1) |
Here,
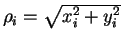 and
and 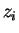 denote, respectively, the radial and
longitudinal coordinate of the
denote, respectively, the radial and
longitudinal coordinate of the 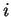 th atom;
th atom; 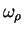 and
and 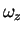 denote,
respectively, the angular frequency in the radial and longitudinal direction; and
denote,
respectively, the angular frequency in the radial and longitudinal direction; and
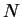 denotes the total number of atoms. We require the anisotropy parameter
denotes the total number of atoms. We require the anisotropy parameter
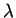 ,
,
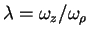 , to be so small that the transverse motion
is ``frozen'' to zero point oscillations. At zero temperature this implies that the
Fermi energy associated with the longitudinal motion of the atoms in the absence of
interactions,
, to be so small that the transverse motion
is ``frozen'' to zero point oscillations. At zero temperature this implies that the
Fermi energy associated with the longitudinal motion of the atoms in the absence of
interactions,
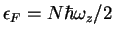 , is much smaller than the separation
between the levels in the transverse direction,
, is much smaller than the separation
between the levels in the transverse direction,
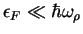 .
This condition is fulfilled if
.
This condition is fulfilled if
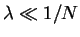 . The outlined scenario can be
realized experimentally with present-day technology using optical traps.
. The outlined scenario can be
realized experimentally with present-day technology using optical traps.
If the Fermi gas is kinematically in 1D, it can be described by an effective 1D
Hamiltonian with contact interactions,
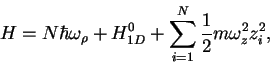 |
(8.2) |
where
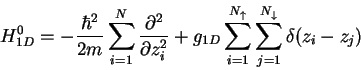 |
(8.3) |
and
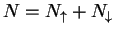 . This effective Hamiltonian accounts for the
interspecies atom-atom interactions, which are parameterized by the 3d
. This effective Hamiltonian accounts for the
interspecies atom-atom interactions, which are parameterized by the 3d 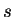 -wave
scattering length
-wave
scattering length 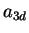 , through the effective 1D coupling constant
, through the effective 1D coupling constant
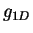 [Ols98,BMO03],
[Ols98,BMO03],
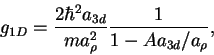 |
(8.4) |
but neglects the typically much weaker 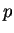 -wave interactions. In
Eq. 8.4,
-wave interactions. In
Eq. 8.4,
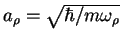 is the characteristic
oscillator length in the transverse direction and
is the characteristic
oscillator length in the transverse direction and
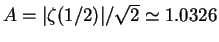 . Alternatively,
. Alternatively, 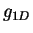 can be expressed through the effective 1D
scattering length
can be expressed through the effective 1D
scattering length 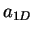 ,
,
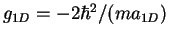 , where
, where
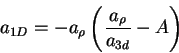 |
(8.5) |
Figure 8.1 shows 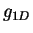 and
and 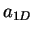 as a
as a
Figure:
Effective 1D coupling constant 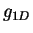 [solid line,
Eq. 8.4], together with effective 1D scattering length
[solid line,
Eq. 8.4], together with effective 1D scattering length 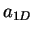 [dashed line, Eq. 8.5] as a function of
[dashed line, Eq. 8.5] as a function of 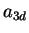 .
.
|
|
function of the 3d 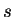 -wave scattering length
-wave scattering length 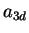 , which can be varied
continuously by application of an external field. The effective 1D interaction is
repulsive,
, which can be varied
continuously by application of an external field. The effective 1D interaction is
repulsive, 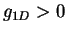 , for
, for
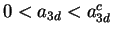 (
(
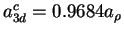 ), and
attractive,
), and
attractive, 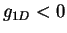 , for
, for
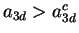 and for
and for 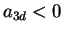 .
By varying
.
By varying 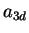 , it is possible to go adiabatically from the weakly-interacting
regime (
, it is possible to go adiabatically from the weakly-interacting
regime (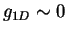 ) to the strongly-interacting repulsive regime (
) to the strongly-interacting repulsive regime (
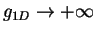 or
or
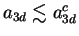 ), as well as from the weakly-interacting
regime to the strongly-interacting attractive regime (
), as well as from the weakly-interacting
regime to the strongly-interacting attractive regime (
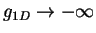 or
or
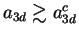 )8.2
)8.2
For two fermions with different spin the Hamiltonian 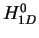 ,
Eq. 8.3, supports one bound state with binding energy
,
Eq. 8.3, supports one bound state with binding energy
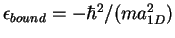 and spatial extent
and spatial extent 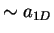 for
for
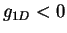 , and no bound state for
, and no bound state for 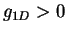 , that is, the molecular state becomes
exceedingly weakly-bound and spatially-delocalized as
, that is, the molecular state becomes
exceedingly weakly-bound and spatially-delocalized as 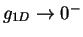 [Ols98,BMO03]. In the following we investigate the properties of a
gas with
[Ols98,BMO03]. In the following we investigate the properties of a
gas with 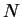 fermions,
fermions,
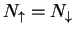 , for both effectively
attractive and repulsive 1D interactions with and without longitudinal
confinement.
, for both effectively
attractive and repulsive 1D interactions with and without longitudinal
confinement.




Next: Homogeneous system
Up: Interacting fermions in highly
Previous: Introduction
Contents
G.E. Astrakharchik
15-th of December 2004
![]() , but to be trapped in different hyperfine states
, but to be trapped in different hyperfine states ![]() , where
, where
![]() represents a generalized spin or angular momentum,
represents a generalized spin or angular momentum,
![]() or
or
![]() . The trapping potential is assumed to be harmonic and axially
symmetric,
. The trapping potential is assumed to be harmonic and axially
symmetric,
![\includegraphics[width=7cm]{1DFermg1D.eps}](1DFermg1D.gif)
![]() -wave scattering length
-wave scattering length ![]() , which can be varied
continuously by application of an external field. The effective 1D interaction is
repulsive,
, which can be varied
continuously by application of an external field. The effective 1D interaction is
repulsive, ![]() , for
, for
![]() (
(
![]() ), and
attractive,
), and
attractive, ![]() , for
, for
![]() and for
and for ![]() .
By varying
.
By varying ![]() , it is possible to go adiabatically from the weakly-interacting
regime (
, it is possible to go adiabatically from the weakly-interacting
regime (![]() ) to the strongly-interacting repulsive regime (
) to the strongly-interacting repulsive regime (
![]() or
or
![]() ), as well as from the weakly-interacting
regime to the strongly-interacting attractive regime (
), as well as from the weakly-interacting
regime to the strongly-interacting attractive regime (
![]() or
or
![]() )8.2
)8.2
![]() ,
Eq. 8.3, supports one bound state with binding energy
,
Eq. 8.3, supports one bound state with binding energy
![]() and spatial extent
and spatial extent ![]() for
for
![]() , and no bound state for
, and no bound state for ![]() , that is, the molecular state becomes
exceedingly weakly-bound and spatially-delocalized as
, that is, the molecular state becomes
exceedingly weakly-bound and spatially-delocalized as ![]() [Ols98,BMO03]. In the following we investigate the properties of a
gas with
[Ols98,BMO03]. In the following we investigate the properties of a
gas with ![]() fermions,
fermions,
![]() , for both effectively
attractive and repulsive 1D interactions with and without longitudinal
confinement.
, for both effectively
attractive and repulsive 1D interactions with and without longitudinal
confinement.