



Next: Conclusions
Up: Interacting fermions in highly
Previous: Homogeneous system
Contents
Using the solutions for the homogeneous two-component 1D Fermi gas,
Figure 8.3:
Energy per particle,
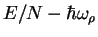 (solid lines),
and size of the cloud,
(solid lines),
and size of the cloud,  (dashed lines), for an inhomogeneous two component 1D
Fermi gas as a function of
(dashed lines), for an inhomogeneous two component 1D
Fermi gas as a function of
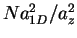 for repulsive (
for repulsive (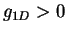 ) and
attractive (
) and
attractive (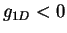 ) interactions.
) interactions.
|
|
we now describe the inhomogeneous gas, Eq. 8.2, within the
LDA [DLO01,MS02,RFZZ03a]. This approximation is applicable if the size
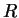 of the cloud is much larger than the harmonic oscillator length
of the cloud is much larger than the harmonic oscillator length  in the
longitudinal direction,
in the
longitudinal direction,
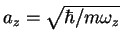 , implying
, implying
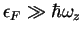 and
and 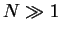 . The chemical potential
. The chemical potential 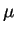 of the inhomogeneous
system can be determined from the local equilibrium condition,
of the inhomogeneous
system can be determined from the local equilibrium condition,
![\begin{displaymath}
\mu=\mu_{hom}[n_{1D}(z)]+\frac{1}{2}m\omega_z^2z^2,
\end{displaymath}](img1720.gif) |
(8.10) |
and the normalization condition
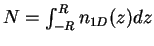 , where
, where 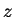 is measured
from the center of the trap,
is measured
from the center of the trap,
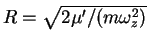 , and
, and
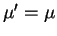 for
for 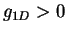 and
and
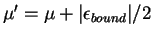 for
for
 . The normalization condition can be reexpressed in terms of the
dimensionless chemical potential
. The normalization condition can be reexpressed in terms of the
dimensionless chemical potential 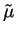 and the dimensionless density
and the dimensionless density
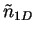 [
[
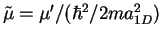 and
and
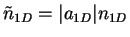 ],
],
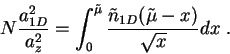 |
(8.11) |
This expression emphasizes that the coupling strength is determined by
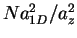 ;
;
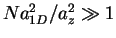 corresponds to the weak coupling and
corresponds to the weak coupling and
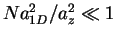 to the strong coupling regime, irrespective of whether the
interactions are attractive or repulsive [MS02].
to the strong coupling regime, irrespective of whether the
interactions are attractive or repulsive [MS02].
Figure 8.3 shows the energy per particle 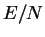 and the size
and the size  of the
cloud as a function of the coupling strength
of the
cloud as a function of the coupling strength
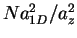 for positive and
negative
for positive and
negative 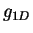 calculated within the LDA for an inhomogeneous two-component 1D
Fermi gas. Compared to the non-interacting gas, for which
calculated within the LDA for an inhomogeneous two-component 1D
Fermi gas. Compared to the non-interacting gas, for which 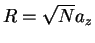 ,
, 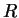 increases for repulsive interactions and decreases for attractive interactions. For
increases for repulsive interactions and decreases for attractive interactions. For
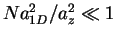 ,
, 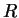 reaches the asymptotic value
reaches the asymptotic value 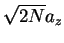 for the
strongly repulsive regime,
for the
strongly repulsive regime,
 , and the value
, and the value
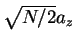 for the strongly attractive regime,
for the strongly attractive regime,
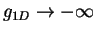 .
The shrinking of the cloud for attractive interactions reflects the formation of
tightly bound molecules. In the limit
.
The shrinking of the cloud for attractive interactions reflects the formation of
tightly bound molecules. In the limit
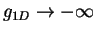 , the energy per
particle approaches
, the energy per
particle approaches
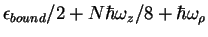 ,
indicating the formation of a molecular bosonic Tonks-Girardeau gas, consisting of
,
indicating the formation of a molecular bosonic Tonks-Girardeau gas, consisting of
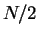 molecules. The size of the cloud shrinks from
molecules. The size of the cloud shrinks from
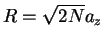 in the strongly
repulsive regime (
in the strongly
repulsive regime (
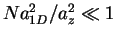 and
and 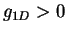 ) to
) to
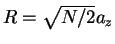 in the
strongly attractive regime (
in the
strongly attractive regime (
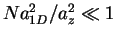 and
and 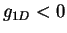 ). We also notice
that, similarly to the homogeneous case, for large attractive interactions the
energy per particle approaches the molecular binding energy
). We also notice
that, similarly to the homogeneous case, for large attractive interactions the
energy per particle approaches the molecular binding energy
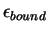 .
.
Using a sum rule approach, the frequency 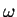 of the lowest compressional
(breathing) mode of harmonically trapped 1D gases can be calculated from the
mean-square size of the cloud
of the lowest compressional
(breathing) mode of harmonically trapped 1D gases can be calculated from the
mean-square size of the cloud
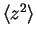 [MS02],
[MS02],
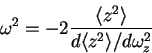 |
(8.12) |
In the weak and strong coupling regime (
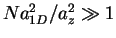 and
and 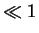 ,
respectively),
,
respectively),
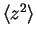 has the same dependence on
has the same dependence on 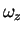 as the
ideal 1D Fermi gas. Consequently,
as the
ideal 1D Fermi gas. Consequently, 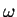 is in these limits given by
is in these limits given by 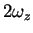 ,
irrespective of whether the interaction is repulsive or attractive.
Solid lines in Fig. 8.3 show
,
irrespective of whether the interaction is repulsive or attractive.
Solid lines in Fig. 8.3 show 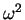 , determined numerically from
Eq. 8.12, as a function of the interaction strength
, determined numerically from
Eq. 8.12, as a function of the interaction strength
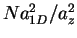 .
A non-trivial behavior of
.
A non-trivial behavior of 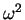 as a function of
as a function of
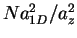 is visible.
To gain further insight, we calculate the first correction
is visible.
To gain further insight, we calculate the first correction 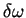 to the
breathing mode frequency
to the
breathing mode frequency 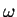
Figure 8.4:
Square of the lowest breathing mode frequency,
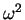 , as a function of the coupling strength
, as a function of the coupling strength
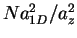 for an
inhomogeneous two-component 1D Fermi gas with repulsive (
for an
inhomogeneous two-component 1D Fermi gas with repulsive (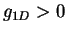 ) and attractive
(
) and attractive
(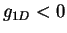 ) interactions determined numerically from Eq. 8.12 (solid
lines). Dashed lines show analytic expansions.
) interactions determined numerically from Eq. 8.12 (solid
lines). Dashed lines show analytic expansions.
|
|
[
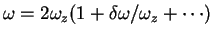 ] analytically for weak repulsive
and attractive interactions, as well as for strong repulsive and attractive
interactions. For the weak coupling regime, we find
] analytically for weak repulsive
and attractive interactions, as well as for strong repulsive and attractive
interactions. For the weak coupling regime, we find
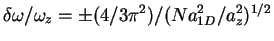 , where the minus sign applies to repulsive
interactions and the plus sign to attractive interactions. For the strong coupling
regime, we find
, where the minus sign applies to repulsive
interactions and the plus sign to attractive interactions. For the strong coupling
regime, we find
^{1/2}$](img1743.gif) for
repulsive interactions and
for
repulsive interactions and
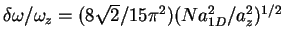 for attractive
interactions (see Table 1.1).Dashed lines in Fig. 8.4 show the resulting analytic expansions for
for attractive
interactions (see Table 1.1).Dashed lines in Fig. 8.4 show the resulting analytic expansions for
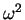 , which describe the lowest breathing mode frequency quite well over a
fairly large range of interaction strengths but break down for
, which describe the lowest breathing mode frequency quite well over a
fairly large range of interaction strengths but break down for
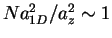 .
.




Next: Conclusions
Up: Interacting fermions in highly
Previous: Homogeneous system
Contents
G.E. Astrakharchik
15-th of December 2004
![\includegraphics[width=7cm]{1DFermiE.eps}](1DFermiE.gif)
![\includegraphics[width=7cm]{1DFermiE.eps}](1DFermiE.gif)
![]() and the size
and the size ![]() of the
cloud as a function of the coupling strength
of the
cloud as a function of the coupling strength
![]() for positive and
negative
for positive and
negative ![]() calculated within the LDA for an inhomogeneous two-component 1D
Fermi gas. Compared to the non-interacting gas, for which
calculated within the LDA for an inhomogeneous two-component 1D
Fermi gas. Compared to the non-interacting gas, for which ![]() ,
, ![]() increases for repulsive interactions and decreases for attractive interactions. For
increases for repulsive interactions and decreases for attractive interactions. For
![]() ,
, ![]() reaches the asymptotic value
reaches the asymptotic value ![]() for the
strongly repulsive regime,
for the
strongly repulsive regime,
![]() , and the value
, and the value
![]() for the strongly attractive regime,
for the strongly attractive regime,
![]() .
The shrinking of the cloud for attractive interactions reflects the formation of
tightly bound molecules. In the limit
.
The shrinking of the cloud for attractive interactions reflects the formation of
tightly bound molecules. In the limit
![]() , the energy per
particle approaches
, the energy per
particle approaches
![]() ,
indicating the formation of a molecular bosonic Tonks-Girardeau gas, consisting of
,
indicating the formation of a molecular bosonic Tonks-Girardeau gas, consisting of
![]() molecules. The size of the cloud shrinks from
molecules. The size of the cloud shrinks from
![]() in the strongly
repulsive regime (
in the strongly
repulsive regime (
![]() and
and ![]() ) to
) to
![]() in the
strongly attractive regime (
in the
strongly attractive regime (
![]() and
and ![]() ). We also notice
that, similarly to the homogeneous case, for large attractive interactions the
energy per particle approaches the molecular binding energy
). We also notice
that, similarly to the homogeneous case, for large attractive interactions the
energy per particle approaches the molecular binding energy
![]() .
.
![]() of the lowest compressional
(breathing) mode of harmonically trapped 1D gases can be calculated from the
mean-square size of the cloud
of the lowest compressional
(breathing) mode of harmonically trapped 1D gases can be calculated from the
mean-square size of the cloud
![]() [MS02],
[MS02],
![\includegraphics[width=0.7\textwidth]{1DFermifreq.eps}](1DFermifreq.gif)