The asymptotic behaviour of the one body density matrix of the Lieb gas is
In order to calculate the momentum distribution one has to calculate the Fourier
transform of it
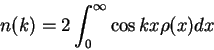 |
(11.2) |
This integral can be calculated numerically up to some cut-off distance ![]() . Let us
suppose, that at distances larger than
. Let us
suppose, that at distances larger than ![]() the asymptotic behavior is valid
(B.1). Than one can calculate the ``tail'' integral
analytically11.1by a substitution
the asymptotic behavior is valid
(B.1). Than one can calculate the ``tail'' integral
analytically11.1by a substitution
![]()
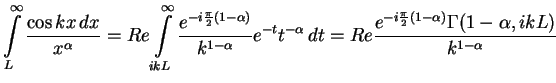 |
(11.3) |
Here the incomplete Gamma function is defined as
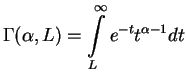 |
(11.4) |
If the if set ![]() then the integral can be simplified11.2
then the integral can be simplified11.2
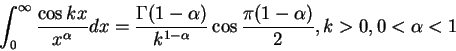 |
(11.5) |
Let us derive an expansion of the incomplete Gamma function in terms of ![]() .
For us it is convenient to use following definition of the function
.
For us it is convenient to use following definition of the function
Integrating it by parts two times we obtain11.3
Here the last term has the same form as (B.6). And can be expanded in a
similar way. Continuation of this expansion leads to formula
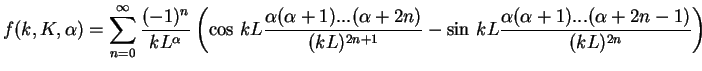 |
(11.8) |
Another way to present it is
Let us write explicitly
| (11.10) |
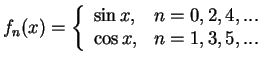 |
(11.11) |
Looking at the structure of the expansion (B.9) one finds out that the
sum converges only is ![]() . The factorial dependence of the numerator on the order
of the term
. The factorial dependence of the numerator on the order
of the term ![]() leads to divergence of the entire sum. Let us find order of the term
leads to divergence of the entire sum. Let us find order of the term
![]() when the summation procedure should be stopped. The condition is
when the summation procedure should be stopped. The condition is
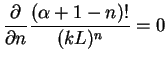 |
(11.12) |
In order to proceed further we will take use of the Stirling formula
| (11.13) |
Simple calculation gives
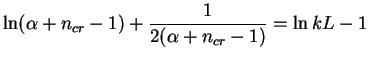 |
(11.14) |
Now we assume that ![]() is much larger than one, so we can neglect the second term.
Finally we obtain
is much larger than one, so we can neglect the second term.
Finally we obtain
| (11.15) |
Another approach for the calculation of the integral is by modifying the integration
contour. First of all, let us expand the cosine into sum of complex exponents
Let us calculate the first integral in this sum.
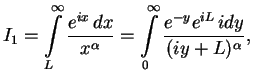 |
(11.17) |
The second integral in (B.16) can be calculated by means of the substitution
![]()
The imaginary parts of the integrals (B.19, B.21) cancel each other and the
result is real
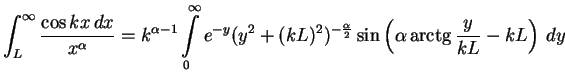 |
(11.22) |