This Hamiltonain can be solved for an arbitrary number of particles spin up
![]() and spins down
and spins down ![]() . The corresponding integral equations
are (
. The corresponding integral equations
are (
![]() )[Yan67]:
)[Yan67]:
The limit ![]() correspond to
correspond to
![]() . In this limit one
can simplify further the system of integral equations by introducing a Fourier
transformation (see also discrete lattice model [Col74]):
. In this limit one
can simplify further the system of integral equations by introducing a Fourier
transformation (see also discrete lattice model [Col74]):
By multiplying first equation from (A.8) by ![]() and integrating over
and integrating over ![]() one obtains expression for the
one obtains expression for the
![]() 10.1
10.1
Setting ![]() one immediately sees that number of spin-down
particles is half of the total number of particles
one immediately sees that number of spin-down
particles is half of the total number of particles
![]() .
.
Inserting (A.10) into second equation from (A.8),
taking into account formula (A.11) and carrying out two
integrations one obtains the integral equation involving only ![]()
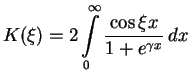 |
(10.13) |
Ones this equation is solved the density and energy are given by
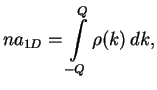 |
(10.14) | ||
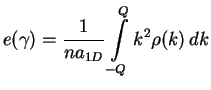 |
(10.15) |
In the strongly interacting limit
![]() and the kernel can be simplified
and the kernel can be simplified
The energy per particle in units of
![$\left[\frac{\hbar^2}{2ma^2}\right]$](img1873.gif) is given by
is given by
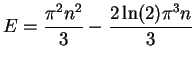 |
(10.17) |
It is possible to express the kernel in terms of ![]() -function (see
Gradstein-Ryzhik). Taking into account the series representation
-function (see
Gradstein-Ryzhik). Taking into account the series representation
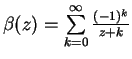 one obtain following result from the
(exact) sum (A.16)
one obtain following result from the
(exact) sum (A.16)
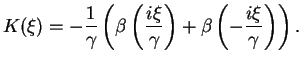 |
(10.18) |
The ![]() -function is defined using the digamma function
-function is defined using the digamma function
![]() . The digamma function
is defined as logarithmic derivative of the Gamma function
. The digamma function
is defined as logarithmic derivative of the Gamma function
![]() .
.
The kernel can be expanded at small and large values of the argument:
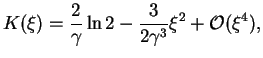 |
(10.19) | ||
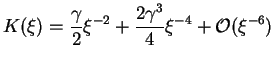 |
(10.20) |