



Next: Expansions
Up: Bethe ansatz solutions
Previous: Repulsive Fermi gas
Contents
In the most general form the integral equations we have to solve is written as
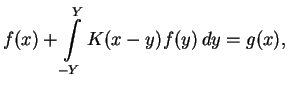 |
|
|
(10.21) |
where 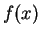 is so far unknown solution,
is so far unknown solution, 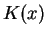 is the kernel,
is the kernel, 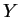 defines the
integration limit,
defines the
integration limit, 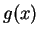 defines the normalization (in LL case it is constant). The
function
defines the normalization (in LL case it is constant). The
function 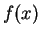 enters twice: once inside the integral and second time outside,
this can be remedied inserting the
enters twice: once inside the integral and second time outside,
this can be remedied inserting the 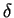 -function:
-function:
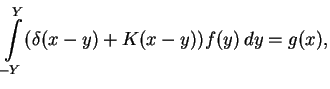 |
|
|
(10.22) |
Now we do discretization with spacing 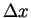 . The equation (A.22) now
can be expressed in the matrix form:
. The equation (A.22) now
can be expressed in the matrix form:
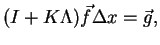 |
|
|
(10.23) |
here 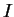 stands for a unity matrix and the diagonal matrix
stands for a unity matrix and the diagonal matrix 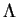 is defined by
the integration method. Now the vector
is defined by
the integration method. Now the vector 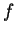 is obtained by multiplication of the
inverse matrix on
is obtained by multiplication of the
inverse matrix on 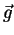 :
:
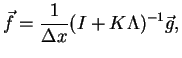 |
|
|
(10.24) |
For a uniform grid very good precision is achieved using the Simpson method. The
matrix 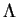 in this case is defined as
in this case is defined as
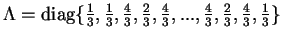 . The residual term of the integration is very
small and can be estimated as
. The residual term of the integration is very
small and can be estimated as
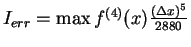 and the error in the energy (which is defined by integrating the solution
and the error in the energy (which is defined by integrating the solution  with the weight proportional to
with the weight proportional to  ) is proportional to the spacing
) is proportional to the spacing 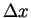 to
the forth power.
to
the forth power.




Next: Expansions
Up: Bethe ansatz solutions
Previous: Repulsive Fermi gas
Contents
G.E. Astrakharchik
15-th of December 2004
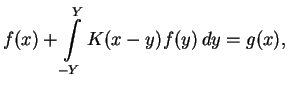
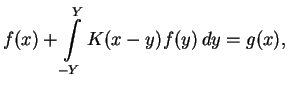
![]() . The equation (A.22) now
can be expressed in the matrix form:
. The equation (A.22) now
can be expressed in the matrix form:
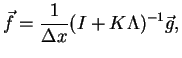
![]() in this case is defined as
in this case is defined as
![]() . The residual term of the integration is very
small and can be estimated as
. The residual term of the integration is very
small and can be estimated as
![]() and the error in the energy (which is defined by integrating the solution
and the error in the energy (which is defined by integrating the solution ![]() with the weight proportional to
with the weight proportional to ![]() ) is proportional to the spacing
) is proportional to the spacing ![]() to
the forth power.
to
the forth power.