Attractive Fermi gas

The Hamiltonain of a two-component fermi gas reads as follows:

$$\hat H = \frac{\hbar^2n^2}{m} \left[-\sum\limits_{i, \sigma}\frac... ...}m}{\hbar^2n}\sum\limits_{i<j}^N\delta(z_{i,\uparrow}-z_{j,\downarrow}) \right]$$ (10.4)

In following we will express all energies in units of $\hbar^2 n^2/2m$ and all distances in units of $\vert a_{1D}\vert$. Let us introduce notation $\gamma = -\frac{g_{1D}m}{\hbar^2n}>0$.

The integral equation for the equation of state is (see [KO75] with notation $\gamma=u/2$, $\rho=\sigma/2$):

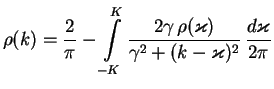$$\rho(k) = \frac{2}{\pi} -\int\limits_{-K}^K\frac{2\gamma\,\rho(\varkappa)}{\gamma^2+(k-\varkappa)^2} \,\frac{d\varkappa}{2\pi}$$ (10.5)

The normalization condition is written as

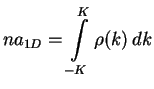$$na_{1D} = \int\limits_{-K}^K \rho(k)\,dk$$ (10.6)

Once the density $\rho(k)$ is known, the energy can be written as

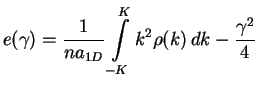$$e(\gamma) = \frac{1}{na_{1D}}\int\limits_{-K}^K k^2\rho(k)\,dk -\frac{\gamma^2}{4}$$ (10.7)