Stationary density-density correlation function

The long-range properties of a weakly interacting one-dimensional bosonic gas can be calculated using the macroscopic representation of the field operator (1.1): $\hat\Psi(x) = \sqrt{\rho_0+\hat\rho^{\prime}(x)}e^{i\hat \varphi(x)}$, where $\rho_0$ is the mean density^1.16 and $\hat\varphi(x)$ is the phase operator. Those operators can be expressed in terms of quasiparticle creation and annihilation operators (see., for example, [PS03] Eqs.(6.65-6.66), and consider a one-dimensional system):

$$\hat \varphi = - i\sum_k \sqrt{\frac{\pi}{\eta \vert k\vert L}} (\hat b_ke^{ikx}-\hat b^\dagger_k e^{-ikx})$$ (1.155)

$$\hat \rho^{\prime} = \sum_k \sqrt{\frac{\eta \vert k\vert}{4\pi L}} (\hat b_ke^{ikx}+\hat b^\dagger_k e^{-ikx}),$$ (1.156)

where we introduced an important parameter describing the interactions between particles:

$$\eta = \frac{2\pi\hbar\rho_0}{Mc}$$ (1.157)

The operators (1.155,1.156) satisfy the commutation rule $[\hat \varphi(x), \hat\rho^{\prime}(x^{\prime})] = -i\delta(x-x^{\prime})$.

Our approach is applicable in a weakly interacting gas $\rho_0\to\infty$. Deep in this regime the speed of sound has a square root dependence on the density $c = \sqrt{g\rho_0/M}$ and the coefficient $\eta$ is large $\eta = 2\pi\hbar\sqrt{\rho_0/Mg}$. In the opposite regime of strong correlations $\rho\to 0$ (TG limit) the bosonic system of impenetrable particles is mapped onto a system of non-interacting fermions [Gir60] with the speed of sound given by the fermi velocity $c_F = \pi\hbar\rho_0/M$ (1.100) and is proportional to the density. In this regime $\eta = 2$. By generalizing the definition of the fermi velocity from the TG regime, where the fermionization of a bosonic system happens, to an arbitary density we obtain a simple interpretation of the parameter (1.157): $\eta = 2c_F/c$. The speed of sound in a system with a repulsive contact potential is not larger than the fermi velocity, thus in LL system (5.1) $\eta \ge 2$. The situation becomes different in a gas of hard-rods of size $a_{1D}$. Presence of an excluded volume makes the available phase space be effectively smaller $L\to L-Na_{1D}$, which in turn renormalizes the speed of sound (see 1.103) and makes it be larger. In this special case of the super-Tonks gas (Sec. 6) the parameter $\eta$ (1.157) can be smaller than $2$.

Following Haldane [Hal81] we introduce a new field $\hat\vartheta(x)$ such that $\nabla\hat\vartheta(x) = \pi[\rho_0+\hat\rho^{\prime}(x)]$. The operator $\hat\vartheta$ satisfy boundary conditions $\hat\vartheta(x+L) = \hat\vartheta(x) +\pi N$ and increases monotonically by $\pi$ each time $x$ passes the location of a particle. Particles are thus taken to be located at the points where $\hat\vartheta(x)$ is a multiple of $\pi$, allowing the density operator to be expressed as $\hat\rho(x) = \nabla\hat\vartheta(x)\{\sum_n \delta[\hat\vartheta(x)-\pi\rho]\}$, or, equivalently,

$$\hat\rho(x) = [\rho_0 + \hat\rho^{\prime}(x)] \sum\limits_{m=-\infty}^\infty \exp[i2m\hat\vartheta(x)]$$ (1.158)

Integrating (1.156) we obtain an expression of this field in terms of creation and annihilation operators:

$$\hat\vartheta(x) = \vartheta_0 + \pi\rho_0 x -i\sum_k \sqrt{\frac... ... L}}\mathop{\rm sign}\nolimits k\, (\hat b_k e^{ikx}-\hat b^\dagger_k e^{-ikx})$$ (1.159)

We will start with calculation of asymptotics of the density-density correlation function:

$$\langle\hat\rho(x)\hat\rho(0)\rangle \approx (\rho_0^2 + \langle\... ...ts_{m,m^{\prime}} \exp[i2(m\hat\vartheta(x)+m^{\prime}\hat\vartheta(0))]\rangle$$ (1.160)

First of all we calculate the contribution coming from density fluctuations $\rho^{\prime}(x)$:

$$\langle\hat\rho^{\prime}(x)\hat\rho^{\prime}(0)\rangle = \langle\... ...b^\dagger_k e^{-ikx}) (\hat b_{k^{\prime}}+\hat b^\dagger_{k^{\prime}}) \rangle$$ (1.161)

The creation and annihilation operators satisfy bosonic commutation relations $[\hat b_k, \hat b^\dagger_{k^{\prime}}] = \delta_{k,k^{\prime}}$ and at zero temperature excitations are absent $\langle \hat b^\dagger_k\hat b_k\rangle = 0$, so in the averaging in Eq. 1.161 we get non zero result only for $\langle \hat b_k\hat b^\dagger_k\rangle = 1$, i.e.

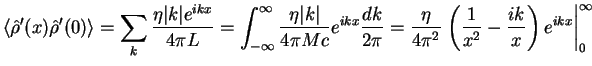$$\langle\hat\rho^{\prime}(x)\hat\rho^{\prime}(0)\rangle =\sum_{k} ... ...pi^2} \left.\left(\frac{1}{x^2}-\frac{ik}{x}\right)e^{ikx}\right\vert _0^\infty$$ (1.162)

We consider contribution only from the lower limit of the integration $k = 0$ and, thus, obtain

$$\langle\hat\rho^{\prime}(x)\hat\rho^{\prime}(0)\rangle =\frac{\eta}{4\pi^2}x^{-2}$$ (1.163)

Now let us calculate the contribution of the phase fluctuations in (1.160):

$$\langle\sum\limits_{m,m^{\prime}} \exp[i2(m\hat\vartheta(x)+m^{\p... ... =~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~$$

$$=\!\!\langle\!\sum\limits_{m,m^{\prime}}\!\!\exp\!\!\left\{\!i2(m... ...ime})-\hat b^\dagger_k(m e^{-ikx}\!+\!m^{\prime}))\right)\!\! \right\}\!\rangle$$ (1.164)

An average of a phonon operator $\hat A$ is gaussian and satisfy an equality $\langle\exp\{\hat A\}\rangle = \exp\{\langle\hat A^2\rangle/2\}$. In this way we can pass from an average of an exponent to an exponent of averaged quantities:

$$\langle\sum\limits_{m,m^{\prime}} \exp[i2(m\hat\vartheta(x)+m^{\p... ...+m^{\prime})\vartheta_0 + i2\pi m\rho_0 x\right\} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$$

$$\exp\!\!\left\{\!\! \sum_k\!\!\frac{\pi\eta}{2\vert k\vert L} \la... ...prime})\!-\!\hat b^\dagger_k(m e^{-ikx}\!\!+\!m^{\prime})) \rangle \!\!\right\}$$ (1.165)

At the zero temperature excitations are absent. This simplifies the calculation as the averaging in (1.165) gives simply $\langle...\rangle =-(me^{-ikx}+m^{\prime})(me^{ikx}+m^{\prime}) = -(m^2+m^{\prime 2}+2mm^{\prime}\cos kx)$. We substitute the summation in the exponent of (1.165) with integration over $\k$:

$$-\sum_k \frac{\pi\eta}{2\vert k\vert L}(m^2+m^{\prime 2}+2mm^{\pr... ...0^\infty\frac{\pi\eta}{2k}(m^2+m^{\prime 2}+2mm^{\prime}\cos kx)\frac{dk}{2\pi}$$ (1.166)

This integral has an infrared divergence unless $m^{\prime}= -m$, so we consider only these terms. Now the integral converges at small $\k$ and takes the leading contribution in the interval $1/x<k<1/\xi$ where $\xi$ is minimal length at which the hydrodinamic theory can be applied. In this region one can neglect the contribution coming from the oscillating cosine term and one has

$$-4m^2\int\limits_{1/x}^{1/\xi} \frac{\pi\eta}{2k}\frac{dk}{2\pi} =-m^2\eta(\ln(1/\xi)-\ln(1/x)) =-\eta m^2\ln(x/\xi)$$ (1.167)

Finally, collecting together (1.163,1.164,1.167) we obtain an expression for the stationary density-density correlation function

$$\frac{\langle\hat\rho(x)\hat\rho(0)\rangle}{\rho_0^2} = \left(1+\... ...}^\infty C_i \cos(2\pi m\rho_0 x) \left(\frac{x}{\xi}\right)^{-\eta m^2}\right)$$ (1.168)