Energy of the Tonks-Girardeau gas

In the very dilute $1D$ regime, when the one-dimensional gas parameter becomes extremely small $n_{1D}\vert a_{1D}\vert\ll 1$, the $1D$ system of bosons can be mapped onto $1D$ system of fermions [Gir60]. In a fermionic system the number of fermions is given by the volume of the fermi sphere (the bosons are mapped onto spinless fermions). In a one-dimensional system this volume degenerates to $2k_F$:

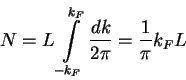$$N = L\int\limits_{-k_F}^{k_F}\frac{dk}{2\pi} = \frac{1}{\pi}k_FL$$ (1.99)

We obtain that the relation of the fermi wave number $k_F$ to the density $n_{1D}$ is linear

$$k_F = \pi n_{1D}$$ (1.100)

The value of $k_F$ fixes the scale for the correlation functions. The static structure factor (5.5) completely changes its behavior at $k=2k_F$. The value of $k_F$ fixes period of oscillations in the pair distribution function (5.4). Being the only spatial length scale in a homogeneous system, $1/k_F$ fixes at the same time value of the healing length $\xi$, and consequently the border at which starts the asymptotic power law decay of the one-body density matrix.

The chemical potential equals to the fermi energy (this is the definition of the fermi energy):

$$\mu_F = \frac{\pi^2 \hbar^2}{2m} n^2_{1D}$$ (1.101)

The energy is obtained by integration of the chemical potential. The energy per particle turns out to be equal to

$$E_F = \frac{\pi^2 \hbar^2}{6m} n^2_{1D}$$ (1.102)