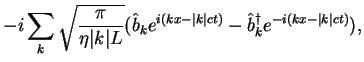 |
(1.169) | ||
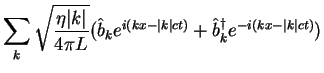 |
(1.170) |
In this Section we develop an approach which allows an estimation of correlations
between different moments of time. We substitute the stationary hydrodynamic
expressions of phase and density operators (1.155,1.156) on time-dependent
hydrodynamic expressions (see, for example, [LP80], Eqs.(24.10)):
It is easy to note (see Eqs. 1.155,1.156) that the time ![]() enters always
in the combination
enters always
in the combination ![]() , which means that time-dependent solution can be
obtained from stationary solution by changing
, which means that time-dependent solution can be
obtained from stationary solution by changing
![]() in integrands and
carrying out integration again. Density fluctuations (1.161) are than
given by
in integrands and
carrying out integration again. Density fluctuations (1.161) are than
given by
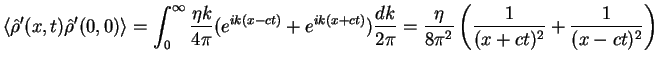 |
(1.171) |
Here again we considered the contribution from the lower limit ![]() .
.
The contribution from the phase fluctuations (1.164) is calculated analogously to
(1.166):
![$\displaystyle -\eta m^2 \left[\int\limits_0^\infty \frac{[1-\cos k(x+ct)]}{k}dk +\int\limits_0^\infty \frac{[1-\cos k(x-ct)]}{k}dk\right]$](img644.gif) |
(1.172) |
The main contribution to integrals comes from momenta
![]() in the
first integral and
in the
first integral and
![]() in the second one. As we are interested in
description of asymptotically large distances condition
in the second one. As we are interested in
description of asymptotically large distances condition ![]() is always fulfilled.
In this conditions the integration gives
is always fulfilled.
In this conditions the integration gives
![$\displaystyle -\frac{1}{2}\eta m^2\left[\ln\frac{x+ct}{\xi}+\ln\frac{x-ct}{\xi}\right]
=-\frac{1}{2}\eta m^2\ln\frac{x^2-c^2t^2}{\xi^2}$](img648.gif) |
(1.173) |
Thus we find that the asymptotic behavior of the time-dependent density-density
correlation function is given by