The phonon dispersion ![]() relation which was used in the derivation
above leads to infrared divergence in some of the integrals (1.166) and was
resolved by truncation of the integral. This problem can be cured using a more
precise Bogoliubov dispersion law:
relation which was used in the derivation
above leads to infrared divergence in some of the integrals (1.166) and was
resolved by truncation of the integral. This problem can be cured using a more
precise Bogoliubov dispersion law:
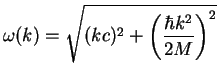 |
(1.175) |
It is easy to see that results for the new dispersion can be obtained by changing
formally
the speed of sound
![]() in definitions of hydrodynamic operators (1.169-1.170. This will lead
to a converging value of the integral (1.166):
in definitions of hydrodynamic operators (1.169-1.170. This will lead
to a converging value of the integral (1.166):
Here we introduced the notation ![]() and
and
![]() .
Let us split the integral (1.176) in two parts:
.
Let us split the integral (1.176) in two parts:
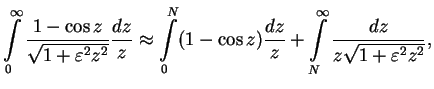 |
(1.177) |
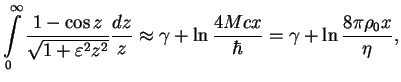 |
(1.178) |
The static density-density correlation function (1.168) (more precisely its ![]() part) is equal to
part) is equal to
The time-dependent result differ from the stationary case (1.179) only by
substitution
![]() in the denominator, as it was already shown
in the calculation with logarithmic accuracy (compare 1.168 and
1.174):
in the denominator, as it was already shown
in the calculation with logarithmic accuracy (compare 1.168 and
1.174):