



Next: Popov's coefficient
Up: Correlation functions in a
Previous: Calculation with non-logarithmic accuracy
Contents
The dynamic form factor is related to the time-dependent density-density correlation
function by the means of the Fourier transformation:
![$\displaystyle S(k,\omega) = \frac{\rho_0}{\hbar}\int\!\!\!\!\int e^{i(\omega t-...
...ft[\frac{\langle\hat\rho(x,t)\hat\rho(0,0)\rangle}{\rho_0^2}-1\right]\, dx\, dt$](img670.gif) |
|
|
(1.181) |
The correlation function was calculated with non-logarithmic accuracy and is given
by formula (1.180). The evaluation of direct Fourier transformation
(1.181) would give us the expression for the dynamic form factor. It turns
out that it is easier to go other way around, i.e. guess the form of the 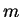 -th
component of
-th
component of 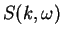
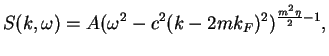 |
|
|
(1.182) |
make the inverse Fourier transformation to go back from 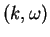 to
to 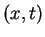 and
comparing obtain result to (1.180) fix the value of the constant
and
comparing obtain result to (1.180) fix the value of the constant  .
Here we use notation
.
Here we use notation
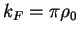 .
We start by doing the integration over momentum.
.
We start by doing the integration over momentum.
 .
We introduce notation
.
We introduce notation
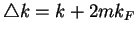 the integral is limited to
the region
the integral is limited to
the region
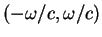 :
:
![$\displaystyle S(x,\omega) =
A c^{m^2\eta-2} e^{i2mk_Fx} \int\limits_{-\omega / ...
...ght)^2-(\triangle k)^2\right]^{\frac{m^2\eta}{2}-1}
\frac{d(\triangle k)}{2\pi}$](img678.gif) |
|
|
(1.183) |
As a reference we use formula 3.771(464/465) from Gradstein-Ryzhik book [GR80]:
The substitution 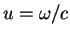 ,
, 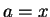 ,
,
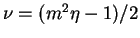 gives an expression
in terms of
gives an expression
in terms of 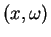
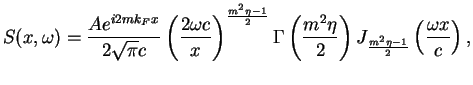 |
|
|
(1.184) |
where 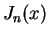 is the Bessel function of the first kind.
The integration over the frequencies
is the Bessel function of the first kind.
The integration over the frequencies
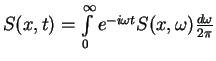 can be done easily done by using the formula (6.699.5) from [GR80]
can be done easily done by using the formula (6.699.5) from [GR80]
and gives
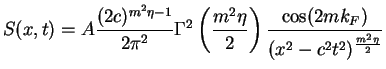 |
|
|
(1.185) |
Comparing this result with (1.180) we fix so far unknown coefficient of the
proportionality to the value
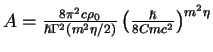 and, finally, obtain
and, finally, obtain
![$\displaystyle S(k, \omega) =
\!\!\sum\limits_{m=1}^\infty\!
\frac{8\pi^2\rho_0 ...
...\!+\!(\omega^2\!\!-\!\!c^2(k\!\!+\!\!2mk_F)^2)^{\frac{m^2\eta}{2}-1}}{2}\right]$](img690.gif) |
|
|
(1.186) |




Next: Popov's coefficient
Up: Correlation functions in a
Previous: Calculation with non-logarithmic accuracy
Contents
G.E. Astrakharchik
15-th of December 2004
![$\displaystyle S(k,\omega) = \frac{\rho_0}{\hbar}\int\!\!\!\!\int e^{i(\omega t-...
...ft[\frac{\langle\hat\rho(x,t)\hat\rho(0,0)\rangle}{\rho_0^2}-1\right]\, dx\, dt$](img670.gif)
![]() -th
component of
-th
component of ![]()
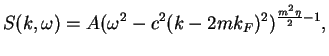
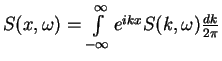 .
We introduce notation
.
We introduce notation
![$\displaystyle S(x,\omega) =
A c^{m^2\eta-2} e^{i2mk_Fx} \int\limits_{-\omega / ...
...ght)^2-(\triangle k)^2\right]^{\frac{m^2\eta}{2}-1}
\frac{d(\triangle k)}{2\pi}$](img678.gif)
![$\displaystyle \int_{0}^{u}{(u^{2}-x^{2})^{\nu-{1\over2}}}
\cos (ax) dx
= {\sqrt...
...1\over2}\right)J_{\nu}(au),\quad
\left[a>0, u>0,\mbox{Re} \nu>-{1\over2}\right]$](img679.gif)
![]() ,
, ![]() ,
,
![]() gives an expression
in terms of
gives an expression
in terms of ![]()
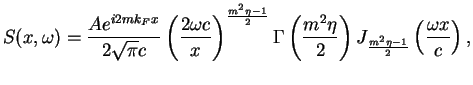
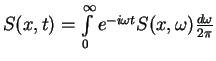 can be done easily done by using the formula (6.699.5) from [GR80]
can be done easily done by using the formula (6.699.5) from [GR80]
![$\displaystyle \int_{0}^{\infty}x^{\nu}\cos (ax) J_{\nu}(bx)\,dx
=2^\nu \frac{b^...
...frac{1}{2}}\quad
\left[0< a<b,\quad \vert\mbox{Re}\,\nu\vert< {1\over 2}\right]$](img687.gif)
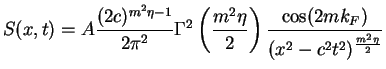
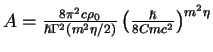 and, finally, obtain
and, finally, obtain