| (1.187) |
The introduced above approach allows us to find the asymptotic behavior of the
one-body density matrix and estimate the coefficient of its decay. Within the first
order of accuracy we split the average as
We first calculate the contribution coming from the phase fluctuations
The average of the exponent can be further developed by using the relation
for the gaussian average
![]() . At zero temperature
excitations are absent and the only nonzero average is
. At zero temperature
excitations are absent and the only nonzero average is
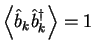 . Thus we obtain
. Thus we obtain
At this point we substitute the phononic excitation spectrum with the proper
Bogoliubov dispersion. This can be done by changing
![]() .
.
Formally this integral is diverging. However, we will take use of the properties of the
![]() -function
-function
As we are interested in long range asymptotical behavior we subtract
(1.191) from the exponent of (1.190) and consider a well-convergent
expression
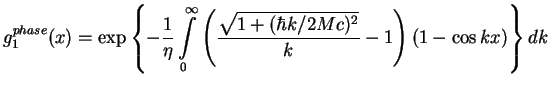 |
(1.192) |
Partial integration together with the notation
![]() and
and ![]() gives
gives
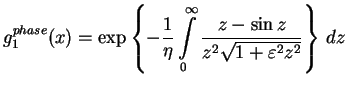 |
(1.193) |
This equation can be calculated with non-logarithmic accuracy at ![]() by splitting the integral in three parts
by splitting the integral in three parts
![]()
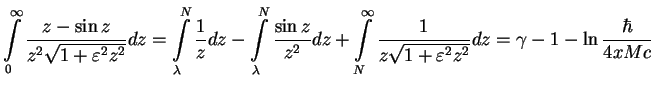 |
(1.194) |
The calculation gives the result
In order to take into account the density fluctuations we develop (1.187)
using Taylor expansion
![]() , so
, so
![]() . Writing the
density operator in terms of creation and annihilation operators (eq. 1.156) we
obtain
. Writing the
density operator in terms of creation and annihilation operators (eq. 1.156) we
obtain
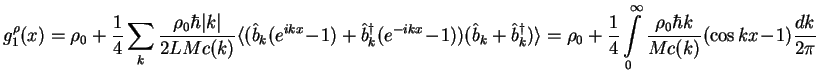 |
We substitute the speed of sound for the Bogoliubov dispersion relation
![]() and express the integral in dimensionless units
and express the integral in dimensionless units
![]() ,
, ![]()
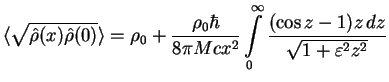 |
(1.196) |
The integral can be evaluated and expanded for small ![]()
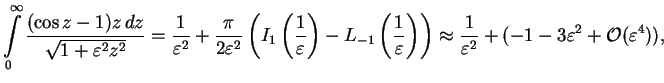 |
(1.197) |
In terms of the parameter ![]() we have
we have
Combining together (1.195) and (1.198) we obtain finally the
expression for the coefficient of the long-range asymptotics
In order to get an expression for the one-body density matrix at a finite
temperature, one should account for thermal quasi-particle excitations. The
long-range excitations are phonons and obey Bose-Einstein statistics
![]() . We are interested at
the long-range behavior of the one-body density matrix, which corresponds to the
limit
. We are interested at
the long-range behavior of the one-body density matrix, which corresponds to the
limit ![]() . In this conditions one can do a Taylor expansion and get
. In this conditions one can do a Taylor expansion and get
![]() . The calculation of the average
(1.188) leads to appearance of an additional term, which depends on the
temperature (compare with (1.189)):
. The calculation of the average
(1.188) leads to appearance of an additional term, which depends on the
temperature (compare with (1.189)):
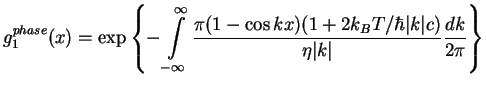 |
(1.200) |
As we will show, the additional thermal suppression becomes dominating and will
change the asymptotic behaviour of ![]() significantly. The effect of the
thermal phase fluctuations can be separated:
significantly. The effect of the
thermal phase fluctuations can be separated:
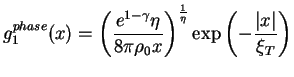 |
(1.202) |
The characteristic thermal decay length ![]() is inversely proportional to the
temperature:
is inversely proportional to the
temperature:
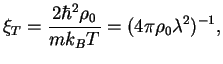 |
(1.203) |