Quantum description of identical particles can be conveniently done in terms of the
creation and annihilation field operators. The operator
![]() puts
a particle into a point
puts
a particle into a point ![]() , while
, while ![]() destroys a particle at the same
point. Field operators can be conveniently presented in terms of creation
destroys a particle at the same
point. Field operators can be conveniently presented in terms of creation ![]() (annihilation
(annihilation
![]() ) operator that puts (destroys) a particle in a single
particle orbital
) operator that puts (destroys) a particle in a single
particle orbital
![]() :
:
Before giving the definition of the correlation functions in terms of the field
operators (1.1), let us discuss how the correlation functions come naturally
from the calculation of the mean values of operators. We shall start with a very
general form of a Hamiltonian consisting of one- and two- body operators
| (1.2) |
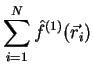 |
(1.3) | ||
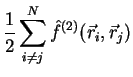 |
(1.4) |
For example, it can be an external potential
![]() (and, thus,
the operator is diagonal the coordinate representation) or it can be the kinetic
energy
(and, thus,
the operator is diagonal the coordinate representation) or it can be the kinetic
energy
![]() (the operator is diagonal in the momentum
representation). A commonly used two-body operator is a particle-particle
interaction is usually defined in the coordinate representation
(the operator is diagonal in the momentum
representation). A commonly used two-body operator is a particle-particle
interaction is usually defined in the coordinate representation
![]() .
.
In the second quantization representation the one-body ![]() and two-body
and two-body
![]() operators are conveniently expressed in terms of the field operators
(1.1).
operators are conveniently expressed in terms of the field operators
(1.1).
Here we assume that the one-body operator can be either local
![]() (like in the case of an
external field), either non local (like in the case of the kinetic energy), so, in
general, we have two arguments
(like in the case of an
external field), either non local (like in the case of the kinetic energy), so, in
general, we have two arguments
![]() . Instead, for the two-body
term we always assume that it is local (i.e. it has a form similar to the
particle-particle interaction energy)
. Instead, for the two-body
term we always assume that it is local (i.e. it has a form similar to the
particle-particle interaction energy)
![]() , so in (1.6) we
have only two arguments instead of four.
, so in (1.6) we
have only two arguments instead of four.
The quantum averages of ![]() and
and ![]() can be extracted from
can be extracted from
![]() and
and ![]() if the correlation functions are
known1.1:
if the correlation functions are
known1.1:
Here
![]() and
and
![]() are the non normalized correlation
functions defined as
are the non normalized correlation
functions defined as
The function
![]() characterizes correlations existing between values of the
field in two different points
characterizes correlations existing between values of the
field in two different points ![]() and
and ![]() . The total phase does not enter in the
definition, but instead the relative phase between two points is important. The
diagonal term
. The total phase does not enter in the
definition, but instead the relative phase between two points is important. The
diagonal term ![]() of (1.9) gives the density of the system
of (1.9) gives the density of the system
![]() , so the trace of
the matrix
, so the trace of
the matrix ![]() gives the total number of particles
gives the total number of particles
![]() . The function
. The function
![]() characterizes the density correlations between
points
characterizes the density correlations between
points ![]() and
and ![]() .
.
It is convenient to introduce dimensionless versions of functions (1.9) and
(1.10):
The function (1.11) is limited to the range ![]() and can be understood as the
probability to destroy a particle at
and can be understood as the
probability to destroy a particle at ![]() and put it at
and put it at ![]() . It is always
possible to put a particle to the place where it was, so
. It is always
possible to put a particle to the place where it was, so
![]() .
The non-diagonal long range asymptotic vanishes in trapped systems and also in
homogeneous systems in the absence of Bose-Einstein condensation
.
The non-diagonal long range asymptotic vanishes in trapped systems and also in
homogeneous systems in the absence of Bose-Einstein condensation
![]() .
.
A more detailed introduction to the analytic properties of the correlation functions can be found, for example, in [Gla63,NG99,GS03a]