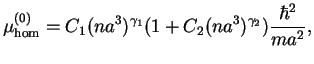Exact solution for 3D ``perturbative'' equation of state

In this Section we will develop theory in three-dimensions for the ``perturbative'' equation of state which we define as:

$$\mu_{\hom}^{(0)}=C_{1}(na^3)^{\gamma_1}(1+C_2(na^3)^{\gamma_2})\frac{\hbar^2}{ma^2},$$ (1.144)

where the $\vert C_2(na^3)^{\gamma_2}\vert\ll 1)$ is the perturbative term.

Within the local density approximation we obtain the chemical potential in a trapped system. The leading term is given by

$$\frac{\mu^{(0)}}{N^{1/3}\hbar\omega}=\frac{1}{\Delta_{3D}^2} \lef... ...1})} {\Gamma(1 + \frac{1}{\gamma_1})}\right){^}\frac{2\gamma_1}{3\gamma_1 + 2},$$ (1.145)

where $\Delta_{3D}$ is the characteristic combination (1.132). The next correction to (1.145) is given by

$$\frac{\mu^{(1)}}{\mu^{(0)}}= 1 + \frac{2C_2}{2 + 3\gamma_1} \frac... ...{3/2} \Gamma(1 + \frac{1}{\gamma_1})}\right)}^{\frac{2\,\gamma_2}{3\gamma_1+2}}$$ (1.146)

The density profile is given by

$$n(r)a^3 = \left(\frac1{C_1}\frac\mu{\hbar^2/ma^2}\left(1-\frac{r^... ...\hbar^2/ma^2}\left(1-\frac{r^2}{R^2}\right)\right)^\frac{1+\gamma_2}{\gamma_1},$$ (1.147)

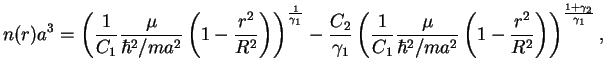where the chemical potential is given by (1.145-1.146), the size of the condensate $R$ is defined in (1.130) while the relation between different units of energy is provided by $N^{1/3}\hbar\omega_{ho} = \Delta_{3D}^2 \hbar^2/ma^2$.

We give an explicit expression for the density in the center of the trap. The leading term is:

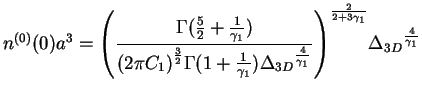$$n^{(0)}(0)a^3 = {\left(\frac{\Gamma(\frac{5}{2}+\frac{1}{\gamma_1... ...}{\gamma_1}}}\right)}^{\frac{2}{2+3\gamma_1}}{\Delta_{3D}}^{\frac{4}{\gamma_1}}$$ (1.148)

The next term is:

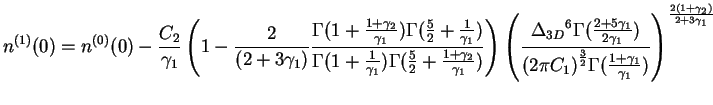$$n^{(1)}(0)=n^{(0)}(0) -\frac{C_2}{\gamma_1} \left(1-\frac{2}{(2+3... ...{1+\gamma_1}{\gamma_1})}\right)}^{\frac{2\left(1+\gamma_2\right)}{2+3\gamma_1}}$$ (1.149)

The scaling approach allows calculation of the frequencies of the collective oscillations. The frequency of the breathing mode is^1.14 $\Omega^2/\omega_{ho}^{2}=3/2~\Xi-1$ in a spherical trap, $\Omega_z^2/\omega_z^2=3-2/\Xi$ and $\Omega_\perp^2/\omega_\perp^2=\Xi$ in a very elongated trap $\omega_z\ll\omega_\perp$. The parameter $\Xi$ defining oscillation frequencies is given by

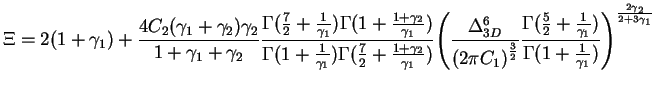$$\Xi = 2(1+\gamma_1) +\frac{4C_2(\gamma_1+\gamma_2)\gamma_2}{1+\ga... ...a_1})}{\Gamma(1+\frac{1}{\gamma_1})}\right)}^{\frac{2\gamma_2}{2 + 3 \gamma_1}}$$ (1.150)

The ``expansion'' equation of states (1.137,1.144) can be naturally applied to the problems, where it is possible to construct a perturbation theory. Another possible application of the discussed above method is to consider the parameters $C_1,C_2,\gamma_1,\gamma_2$ as variational and fix them by fitting to an equation of state, where an exact solution to the LDA problem is not known. An arbitrary equation of state can be expanded as (1.137,1.144) in any point, for example, by demanding that the first three derivatives of the function and the function itself coincide with the ones calculated from the (1.137,1.144). The four conditions of the continuity fixes four parameters.