



Next: Exact solution for 3D
Up: Local Density Approximation
Previous: General method
Contents
Exact solution for 1D ``perturbative'' equation of state
We will start from very general equation of state of a homogeneous system which can
be found in any type of first-order perturbation theory. In the zeroth approximation
one has1.121.13:
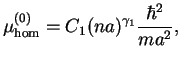 |
|
|
(1.136) |
here 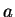 is unit of length,
is unit of length, 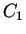 is a numerical coefficient of the
leading term in the chemical potential and
is a numerical coefficient of the
leading term in the chemical potential and 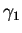 is the power of the
dependence on the gas parameter
is the power of the
dependence on the gas parameter 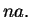 The next term of perturbation in
general can be written as
The next term of perturbation in
general can be written as
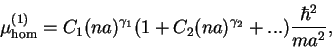 |
(1.137) |
where
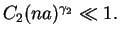 We will use local density approximation
(Sec. 1.6) in order to obtain properties of trapped system. The equation
(1.126) can be inverted by using (1.137) to obtain the density profile
We will use local density approximation
(Sec. 1.6) in order to obtain properties of trapped system. The equation
(1.126) can be inverted by using (1.137) to obtain the density profile
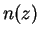 :
:
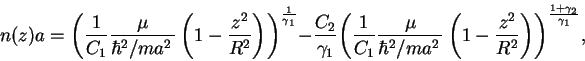 |
(1.138) |
here size of the cloud 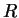 is related to the chemical potential
is related to the chemical potential
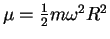 (1.130).
(1.130).
The value of the chemical potential is fixed by the normalization condition
(1.127). It is convenient to make use of the integral equality [GR80]
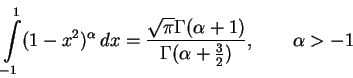 |
(1.139) |
Thus we have restriction on the polytropic indices
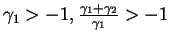 . If those conditions are
satisfied, then the leading contribution to the chemical potential is given by
. If those conditions are
satisfied, then the leading contribution to the chemical potential is given by
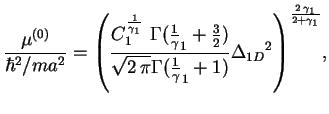 |
|
|
(1.140) |
where 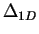 is the characteristic parameter of a one-dimensional trapped
gas defined by (1.135).
is the characteristic parameter of a one-dimensional trapped
gas defined by (1.135).
In the next order of accuracy the chemical potential is given by
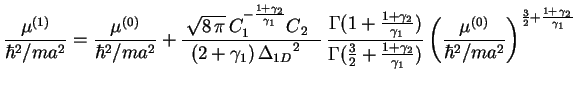 |
|
|
(1.141) |
The mean square displacement
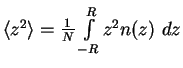 is directly related to the
potential energy of the oscillator confinement and is given by
is directly related to the
potential energy of the oscillator confinement and is given by
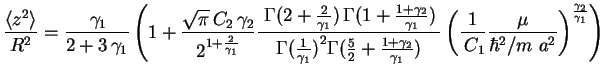 |
|
|
(1.142) |
The frequencies of the collective oscillations can be predicted within LDA. The
frequency of the breathing mode is inferred from the derivative of the mean square
displacement
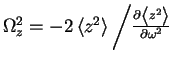 [MS02] and equals to
[MS02] and equals to
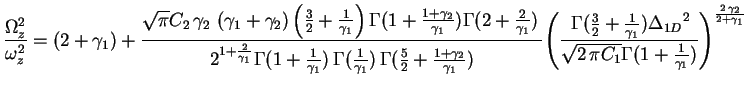 |
|
|
(1.143) |
The obtained formula is very general and gives an insight to many interesting cases
where the perturbation theory can be developed. In the table
(1.1) we summarize some of the examples.
Table 1.1:
Summary for some of one-dimensional models where the expansion of the
equation of state is known. The first column labels the considered model. The
coefficients of the expansion are given in columns 2-5. The last column gives the
predictions for the oscillation frequencies calculated calculated as (1.143).
The parameter 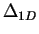 is defined by (1.132). Note that the presence
of a term in the chemical potential independent of the density (for example, binding
energy of a molecule) does not modify the frequencies of oscillations and is
ignored.
is defined by (1.132). Note that the presence
of a term in the chemical potential independent of the density (for example, binding
energy of a molecule) does not modify the frequencies of oscillations and is
ignored.
| Limit |
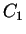 |
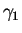 |
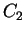 |
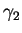 |
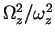 |
| Lieb-Liniger: weak interaction |
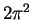 |
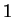 |
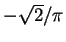 |
-1/2 |
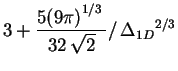 |
| Lieb-Liniger: strong interaction |
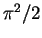 |
2 |
-8/3 |
1 |
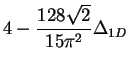 |
| Attractive Fermi gas: strong interaction |
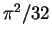 |
2 |
2/3 |
1 |
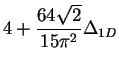 |
| Attractive Fermi gas: weak interaction |
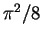 |
2 |
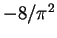 |
-1 |
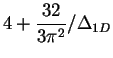 |
| Repulsive Fermi gas: strong interaction |
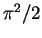 |
2 |
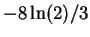 |
1 |
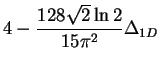 |
| Repulsive Fermi gas: weak interaction |
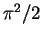 |
2 |
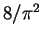 |
-1 |
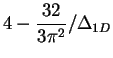 |
| Gas of Hard-Rods |
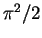 |
2 |
8/3 |
1 |
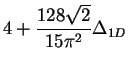 |
|




Next: Exact solution for 3D
Up: Local Density Approximation
Previous: General method
Contents
G.E. Astrakharchik
15-th of December 2004
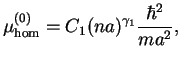
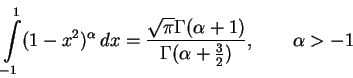
![]() . If those conditions are
satisfied, then the leading contribution to the chemical potential is given by
. If those conditions are
satisfied, then the leading contribution to the chemical potential is given by
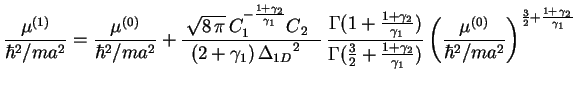
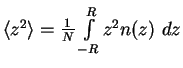 is directly related to the
potential energy of the oscillator confinement and is given by
is directly related to the
potential energy of the oscillator confinement and is given by
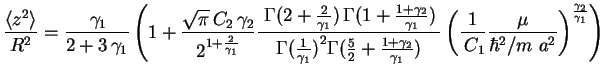
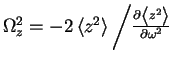 [MS02] and equals to
[MS02] and equals to