General method

In the local density approximation one assumes that the chemical potential $\mu$ is given by sum of the local chemical potential $\mu _{hom}$, which is the chemical potential of the uniform system, and the external field:

$$\mu = \mu_{\hom}(n(\r)) + V_{ext}(\r)$$ (1.126)

The local chemical potential $\mu _{hom}$ is defined by the equation of state in absence of the external field and accounts for the interaction between particles and partially for the kinetic energy.

The value of the chemical potential $\mu$ is fixed by the normalization condition

$$N = \int n(\r)\,{d\vec r},$$ (1.127)

where the density profile is obtained by inverting the density dependence of the local chemical potential $n = \mu_{\hom}^{-1}$.

Once the chemical potential $\mu$ is known a lot of useful information can be inferred: the density profile, energy, size of the cloud, density moments $\langle r^2\rangle$, etc.

In the following we will always consider a harmonic external confinement:

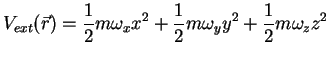$$V_{ext}(\r) = \frac{1}{2}m\omega_x x^2+\frac{1}{2}m\omega_y y^2+\frac{1}{2}m\omega_z z^2$$ (1.128)

The normalization condition (1.127) becomes:

$$N= \int\!\!\!\!\int\!\!\!\!\int\mu_{\hom}^{-1}\left[\mu-\frac{1}{2}m\omega_x x^2-\frac{1}{2}m\omega_y y^2-\frac{1}{2}m\omega_z z^2\right]\,dx dy dz$$ (1.129)

The sizes of the cloud in three directions $R_x,R_y,R_z$ is fixed by the value of the chemical potential and corresponding frequencies of the harmonic confinement through relation:

$$\mu = \frac{1}{2}m\omega_x R_x^2=\frac{1}{2}m\omega_y R_y^2=\frac{1}{2}m\omega_z R_z^2$$ (1.130)

We express the distances in the trap in units of the size of the cloud: $\tilde r = (x/R_x,y/R_y,z/R_z)$ and in front of the integral (1.129) we have the geometrical average $R_xR_yR_z = R^3$ appearing. It means that the trap frequencies (even if the trap is not spherical) enter only through combination $\omega_{ho} = (\omega_x\omega_y\omega_z)^{1/3}$ and the oscillator lengths correspondingly through parameter $a_{ho} =\sqrt{\hbar/m\omega}$. Now the integral is to be taken inside a sphere of radius $1$ and is symmetric in respect to $\tilde r$. It follows immediately, that the normalization condition (1.129) in general can be written as

$$\Delta_{3D}^3 = \tilde\mu^{3/2} \int_0^1 a^3\mu_{\hom}^{-1}\left[... ...^2}{ma^2} \tilde\mu\Delta_{3D}^2(1-\tilde r^2)\right]4\pi\tilde r^2\,d\tilde r,$$ (1.131)

here the dimensionless chemical potential $\tilde\mu$ is obtained by choosing $\frac{N^{1/3}}{2}\hbar\omega_{ho}$ as the unit of energy in the trap, the density in a homogeneous system $\mu_{\hom}^{-1}$ is measured in units of $a^{-3}$, where $a$ is a length scale convenient for the homogeneous system (for example it can be equal to the $s$-wave scattering length $a_{3D}$), chemical potential (i.e. the argument of the inverse function $\mu_{\hom}^{-1}$) is measured in units of $\hbar^2/ma^2$, and, finally, the characteristic parameter $\Delta_{3D}$ is defined as

$$\Delta_{3D} = N^{1/6}\frac{a}{a_{ho}}$$ (1.132)

From the Eq. 1.131, which is basically a dimensionless version of Eq. 1.129 we discover there is a scaling in terms of the characteristic parameter $\Delta_{3D}$. In other words systems having different number of particles and oscillator frequencies will have absolutely the same density profile and other LDA properties (once expressed in the correct units as discussed above) if they have equal values of parameter (1.132).

A similar procedure can be carried in a one-dimensional case (we choose the $z$ axis), where the normalization condition reads as

$$N = \int\mu_{\hom}^{-1}\left[\mu-\frac{1}{2}m\omega_zz^2\right]\,dz$$ (1.133)

Its dimensionless form is obtained by measuring the energies in the trap in units of $\frac{1}{2}N\hbar\omega_z$

$$\Delta_{1D} =\tilde\mu^{1/2}\int_{-1}^1 a\mu_{\hom}^{-1}\left[\frac{\hbar^2}{ma^2} \tilde\mu\Delta_{1D}^2(1-\tilde z^2)\right]\,d\tilde z,$$ (1.134)

and the one-dimensional characteristic parameter is related to the number of particles as

$$\Delta_{1D} = \frac{N^{1/2}a}{a_z}$$ (1.135)