Variational derivation of the GPE

Let us consider $N$ identical bosons in an external potential $V_{ext}$. For $T\ll T_c$ all particle stay in the ground state of the Hamiltonian:

$$\hat H = \sum\limits_{i=1}^{N} \left[\frac{\hat p_i^2}{2m}+V_{ext... ..._i)\right] +\frac{1}{2}\sum\limits_{i\ne j}^N V_{int}({{\vec r}_i-{\vec r}_j}),$$ (1.107)

At low temperatures, namely when the de Broglie wavelength $\lambda_T$ becomes much larger than the range of $V_{int}(r_{ij})$, only s-wave scattering between pairs of bosons remains significant, and we can approximate $V_{int}(r_{ij})$ by a pseudopotential (1.86).

Generally, the ground state of $\hat H$ cannot be determined exactly. In the absence of interactions however, it is a product state: all the bosons are in the ground state of the single particle Hamiltonian. In the presence of weak interactions, one still can approximate the ground state of $\hat H$ by a product state:

$$\vert\phi_0\rangle =\vert\psi(1)\rangle ... \vert\psi(N)\rangle,$$ (1.108)

where all bosons are in the same state $\vert\psi\rangle$^1.11.

Obviously, $\vert\phi_0\rangle$ is symmetric with the respect to exchange of particles and has the correct symmetry for a system of bosons. Contrary to the non-interacting case, $\vert\psi\rangle$ is no longer the ground state of the single particle Hamiltonian, but has to be determined by minimizing the energy:

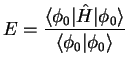$$E = \frac{\langle\phi_0\vert\hat H\vert\phi_0\rangle}{\langle\phi_0\vert\phi_0\rangle}$$ (1.109)

Let us calculate the value of (1.107) averaged over the Fock state (1.108). In the coordinate representation the external potential energy becomes:

$$\begin{eqnarray*} \langle\phi_0\vert\!\sum\limits_{i=1}^N V_{ext}({\vec r}_i)\ve... ...dR} \!=\!N\!\!\int\!\!\psi^*(\r) V_{ext}(\r) \psi(\r)\;{d\vec r} \end{eqnarray*}$$

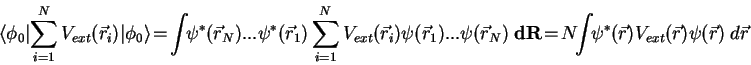
For the interaction between the particles we obtain:

$$\begin{eqnarray*} \langle\phi_0\vert\sum\limits_{i\ne j}^N \frac{1}{2}V_{int}(r_... ...vert{\vec r}\!-\!\r'\vert)\psi(\r)\psi(\r')\;{d\vec r}{d\vec r}' \end{eqnarray*}$$

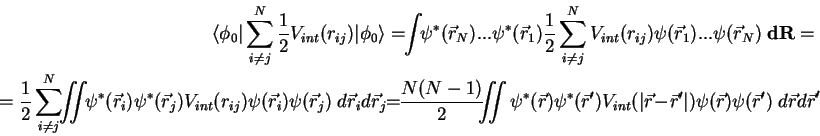
Thus we obtain the expression of the total Hamiltonian in the first quantization (see, also, (1.16))

$$\langle\hat H\rangle\!\! =\!\!N\!\!\int\!\! \psi^*\!(\r)\!\left(\... ...r)\psi^*\!(\r') V_{int}(\vert\r-\r'\vert)\psi(\r)\psi(\r')\;{d\vec r}{d\vec r}'$$ (1.110)

We now look for the minimum of the energy $\langle\phi_0\vert\hat H\vert\phi_0\rangle$ keeping the normalization fixed $\langle\phi_0\vert\phi_0\rangle = 1$. Because $\psi$ in general is a complex number, we can consider the variations $\delta\psi$ and $\delta\psi^*$ as independent. Using the method of Lagrange multipliers, the approximate ground state $\vert\phi_0\rangle$ has to satisfy:

$$\delta\left[\langle\phi_0\vert\hat H\vert\phi_0\rangle\right]-\mu\delta\langle\phi_0\vert\hat H\vert\phi_0\rangle = 0,$$ (1.111)

where $\mu$ is the Lagrange multiplier associated with the constraint $\langle\phi_0\vert\phi_0\rangle = 1$.

Inserting the expression (1.110) in equation (1.111) and setting to zero the linear term $\delta\psi^*$ we yield:

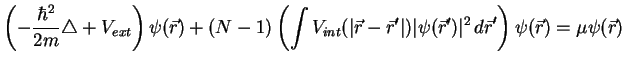$$\left(-\frac{\hbar^2}{2m}\triangle+V_{ext}\right)\psi(\r) +(N-1)\... ...\vert\r-\r'\vert)\vert\psi(\r')\vert^2\,{d\vec r}'\right)\psi(\r) = \mu\psi(\r)$$ (1.112)

Now we use that the properties of the $s$-wave scattering at the discussed conditions can be described by using the pseudopotential (1.86) and, finally, obtain

$$\left(-\frac{\hbar^2}{2m}\triangle+V_{ext}\right)\psi(\r)+(N-1)g_{3D}\vert\psi(\r)\vert^2\psi(\r) = \mu\psi(\r)$$ (1.113)

This is the Gross-Pitaevskii equation [Gro61,Pit61]. It has a straightforward interpretation: each boson evolves in the external potential $V_{ext}$ and in the mean-field potential produced by the other $N-1$ bosons.

Let us clarify the meaning of the parameter $\mu$, which was introduced formally as a Lagrange multiplier. Multiplying GP equation (1.113) by $\psi^*(r)$ and by carrying out an integrating over $\r$ we have:

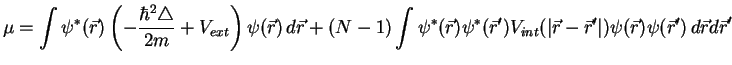$$\mu = \int \psi^*(\r)\left(-\frac{\hbar^2\triangle}{2m}+V_{ext}\r... ...*(\r)\psi^*(\r')V_{int}(\vert\r-\r'\vert)\psi(\r)\psi(\r')\,{d\vec r}{d\vec r}'$$ (1.114)

A direct comparison to (1.110) shows that $\mu = \frac{d}{d N} \langle\phi_0\vert\hat H\vert\phi_0\rangle$ (number of considered particles is large) and thus $\mu$ has a physical meaning of the chemical potential.

An alternative way is to normalize the wave function to the number of particles in the system $\langle\phi_0\vert\phi_0\rangle = N$. In this normalization GPE reads as ($N\gg 1$):

$$\left(-\frac{\hbar^2}{2m}\triangle+V_{ext}\right)\psi(\r)+g_{3D}\vert\psi(\r)\vert^2\psi(\r) = \mu\psi(\r)$$ (1.115)