The mean-field relation of the coupling constant in 1D, ![]() and in 2D,
and in 2D,
![]() , to the three dimensional scattering length
, to the three dimensional scattering length ![]() in restricted
geometries can be found by repeating the derivation given in Sec. 1.5.1
while assuming that the order parameter
in restricted
geometries can be found by repeating the derivation given in Sec. 1.5.1
while assuming that the order parameter ![]() can be factorized. We start from the
energy functional (1.110)
can be factorized. We start from the
energy functional (1.110)
In the presence of an external confinement along one direction (disk-shaped
condensate)
![]() we assume a gaussian ansatz for the
wave function
we assume a gaussian ansatz for the
wave function
![]() with
with
![]() being ground state
wave function of a harmonic oscillator. The integration over
being ground state
wave function of a harmonic oscillator. The integration over ![]() in (1.116) can be easily done by using following properties of the gaussian
function
in (1.116) can be easily done by using following properties of the gaussian
function ![]() :
:
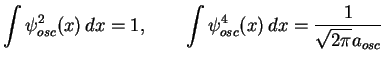 |
(1.119) |
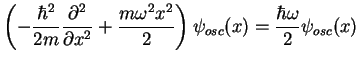 |
(1.120) |
Integrating out ![]() from the GP energy functional (1.116) and
doing the variational procedure (1.117) we obtain the Gross-Pitaevskii
equation in a quasi two dimensional system
from the GP energy functional (1.116) and
doing the variational procedure (1.117) we obtain the Gross-Pitaevskii
equation in a quasi two dimensional system
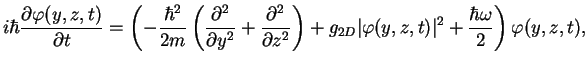 |
(1.121) |
If the external potential restricts the motion in two dimensions (i.e. in a
cigar-shaped condensate) and the confinement is so strong that no excitations in the
radial direction are possible, the wave function gets factorized in the following
way:
![]() . The explicit integration in
(1.116) over
. The explicit integration in
(1.116) over ![]() and
and ![]() leads to one-dimensional Gross-Pitaevskii
equation
leads to one-dimensional Gross-Pitaevskii
equation
Here ![]() denotes effective one-dimensional coupling constant
denotes effective one-dimensional coupling constant
Comparing it with the definition of the 1D coupling constant
![]() (1.69) we find the mean-field relation of one-dimensional
scattering length
(1.69) we find the mean-field relation of one-dimensional
scattering length ![]() to the three-dimensional scattering length
to the three-dimensional scattering length ![]() and
oscillator length
and
oscillator length ![]() :
: