Scattering on a pseudopotential

In a one-dimensional system the contact $\delta$-potential is a ``good'' potential and the problem of a scattering on it is solved in a standard manner, as described in Sec. 1.3.3.1 without any special tricks. The situation is different in three-dimensions where the $\delta$-potential has to be regularized (refer to Sec.1.3.4.1) in order to avoid a possible divergence which can be caused by the behavior of a symmetric solution (1.39).

The $\delta$-pseudopotential turns out to be highly useful theoretical tool. Indeed the commonly used Gross-Pitaevskii equation corresponds to pseudopotential interaction $V_{int}(z)=g_{1D}\delta(z)$. A system of particles with $\delta$-pseudopotential interaction (5.1) is one of few exactly solvable one dimensional quantum systems.

The Schrödinger equation (1.61) of the scattering on a pseudopotential

$$-\frac{\hbar^2}{2\mu}f''(z) + g_{1D}\delta(z) f(z) = {\cal E}f(z),$$ (1.64)

In the region $\vert z\vert>0$ it takes form of a free particle propagation $f''(z) + k^2f(z) = 0$ with the even solution given by

$$f(z) = \cos(k\vert z\vert+\Delta)$$ (1.65)

We are left with the only point $z=0$, where the scattering potential is nonzero $V_{int}(r)\ne 0$. The infinite strength of the $\delta$-potential makes the first derivative of the potential be discontinuous. Indeed, the proper boundary condition can be obtained by integrating the equation (1.64) from infinitesimally small $-\varepsilon$ up to $+\varepsilon$. The integral of the continuous function $f_2(z)$ is proportional to $\varepsilon$ and vanishes in the limit $\varepsilon\to 0$. Instead the $\delta$-function extracts the value of the function in zero and one obtains the relation

$$f'(\varepsilon) - f'(-\varepsilon) = \frac{2\mu g_{1D}}{\hbar^2} f(0)$$ (1.66)

This boundary condition for the solution (1.65) provides a relation between the scattering phase $\Delta$ and the momentum $\k$ of an incident particle

$$\Delta(k) = - \mathop{\rm arcctg}\nolimits \frac{\hbar^2 k}{\mu\,g_{1D}}$$ (1.67)

Taking the limit of the low energy scattering from (1.63) one obtains the value of the scattering length

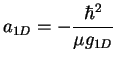$$a_{1D} = -\frac{\hbar^2}{\mu g_{1D}}$$ (1.68)

This expression can be read the other around: for equal mass particles $\mu = m/2$ the strength of the potential $g_{1D}$ in a one-dimensional homogeneous system is related to the value of the one-dimensional coupling constant as

$$g_{1D} = -\frac{2\hbar^2}{ma_{1D}}$$ (1.69)

It is interesting to note, that the sign in the relation of the scattering length to the coupling constant is opposite to the one of a three dimensional system. In $3D$ positive scattering length corresponds to repulsion and negative one to attraction. Another difference is that the 3D coupling constant is directly proportional to the scattering length, although $g_{1D}$ is inversely proportional to $a_{1D}$.

In terms of $a_{1D}$ the phase (1.67) becomes

$$\Delta(k) = -\mathop{\rm arcctg}\nolimits ka_{1D}$$ (1.70)

The scattering solution (1.65) gets written as:

$$f(z) = \cos(k\vert z\vert+\mathop{\rm arcctg}\nolimits ka_{1D})$$ (1.71)

In the low energy limit $k\to 0$ the phase (1.70) can be expanded $\Delta(k) = -\pi/2+ka_{1D}+{\cal O}(k^2)$ and the scattering solution becomes simply $f(z) = k(\vert z\vert+a_{1D})$. One sees that the one-dimensional scattering length coincides with the position of the first node of the analytic continuation of the low-energy solution^1.7.