Scattering on a 1D square well potential

In this section we will consider scattering on a one-dimensional square well. The potential is similar to the one of the soft sphere with the difference that now the potential is attractive:

$$V^{SW}(z) = - V_0\,\Theta(R^2-z^2),$$ (1.72)

where $R$ is the range of the potential. In the region $\vert z\vert < R$ the kinetic energy of the slow particle can be neglected

$$f''(z) + V_0 f(z) = 0$$ (1.73)

All solutions can be decomposed into a sum of even and odd solutions distinguished by the boundary condition at zero which can be either $f(0) = 0$ or $f'(0) = 0$. We choose the state with the minimal energy, i.e. $f'(0) = 0$, which leads to the solution of the form

$$f(z) = A\cos(\sqrt{V_0}\,z),\qquad \vert z\vert<R$$ (1.74)

In the other region $\vert z\vert>R$ the interaction potential is absent and the solution is a plain wave

$$f(z) = B\sin(kz+\delta_0),\qquad \vert z\vert<R$$ (1.75)

The scattering phase can be defined from the continuity condition of the logarithmic derivative at the matching distance $R$. This condition reads as

$$\frac{f'(R)}{f(R)}= -\sqrt{V_0} \mathop{\rm tg}\nolimits (\sqrt V_0 R) = k \mathop{\rm ctg}\nolimits (kR+\delta_0)$$ (1.76)

Eq. (1.76) fixes the dependence of the phase on the wave number of the scattering particle:

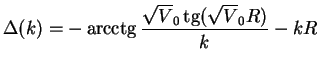$$\Delta(k) = -\mathop{\rm arcctg}\nolimits \frac{\sqrt V_0 \mathop{\rm tg}\nolimits (\sqrt V_0 R)}{k}-kR$$ (1.77)

Finally, from (1.63) we obtain the expression for the scattering length on the 1D square well potential:

$$a_{1D} = R\left(1+\frac{\mathop{\rm ctg}\nolimits (\sqrt V_0 R)}{\sqrt V_0 R}\right)$$ (1.78)