As it was discussed above, in Secs. 1.3.2.1-1.3.2.3, scattering on
different short-ranged potentials in the low-energy limit is universal, i.e. depends
essentially on one parameter, the scattering length and the particular shape of the
potential is of no large importance. Thus it is very useful to relate scattering on
all those potentials to a scattering on a simple ![]() -potential. In other words
instead of considering a particular shape of the interaction potential, we give the
description it terms of a free scattering solution at
-potential. In other words
instead of considering a particular shape of the interaction potential, we give the
description it terms of a free scattering solution at ![]() with an appropriate
boundary condition at
with an appropriate
boundary condition at ![]() , which takes properly into account the scattering length
and, thus, the interaction potential.
, which takes properly into account the scattering length
and, thus, the interaction potential.
In one dimensional case the application of this scheme is straight as the
Schrödinger equation for two particles can be directly solved, as it is explained
in the Sec. 1.3.3.2. In three dimensions the situation is more complicated as
the behavior of the solution (1.39) is not compatible with scattering on a
![]() -potential and special adjustments should be made.
-potential and special adjustments should be made.
Let us revise the solution of the Schrödinger equation in the limit of low energy
scattering. From the definition of the three-dimensional scattering length
(1.44) it follows that the scattering solution vanishes at the distance ![]() . Thus we define the scattering function of the pseuodopotential in such a
way that it satisfies the free scattering equation in the region
. Thus we define the scattering function of the pseuodopotential in such a
way that it satisfies the free scattering equation in the region ![]() :
:
We will use the expression (1.45) to approach the ![]() limit:
limit:
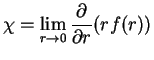 |
(1.83) |
We can now modify Eq. 1.81 in such a way that it satisfies the correct
boundary condition (1.82). By inserting (1.82) into (1.81) we
obtain1.8
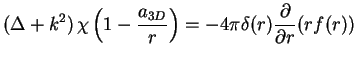 |
(1.84) |
The pseudopotential (1.85,1.86) was used by Olshanii [Ols98] to solve quasi one dimensional scattering problem in a tight harmonic transverse confinement.
Finally, the wave function ![]() satisfies the equation1.9:
satisfies the equation1.9:
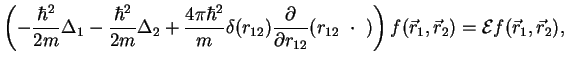 |
(1.87) |