Scattering on a soft sphere potential

In order to test the universality assumption and if the details of the potential are important it is useful to have a potential, where the range of the potential $R$ can be varied while keeping the $s$-wave scattering length constant. In the case of the hard-sphere (Sec. 1.3.2.2) both distances are the same. The easiest way to modify the hard sphere potential (1.48) in such a way that it has desired properties is to make the height of the potential finite. The resulting potential is called the soft-sphere (SS) potential:

$$V^{SS}(r) = \left\{ {\begin{array}{ll} V_0,& r < R\\ 0, & r \ge R \end{array}} \right.$$ (1.52)

where $V_0$ is positive.

The Schrödinger equation (1.41) for a pair of particles in the center of mass system is given by

$$\left\{ {\begin{array}{ll} u''(r)+(k^2-\varkappa ^2)u(r) = 0,& r<R\\ u''(r)+k^2u(r) = 0, &r\ge R \end{array}} \right.,$$ (1.53)

where we express the energy of the incident particle in terms of the wave number $k^2 = m{\cal E}/\hbar^2$ and introduce a characteristic wave number related to the height of the potential:

$$\varkappa ^2 = mV_0/\hbar^2$$ (1.54)

We are interested in scattering at small energy, so ${\cal E}<V_0$. For convenience we introduce ${\cal K}^2=\varkappa ^2-k^2$, where ${\cal K}$ is real. The second equation out of the pair (1.53) has a free wave solution which extends with the same amplitude to large distances, although the first equation has a decaying solution expressed in terms of the hyperbolic sinus:

$$u(r) = \left\{ {\begin{array}{ll} A\mathop{\rm sh}\nolimits ({\cal K}r+\delta_1),& r<R\\ B\sin(kr+\delta), &r\ge R \end{array}} \right.$$ (1.55)

The phase $\delta_1$ must be equal to zero in order to obtain a solution which is not divergent at $r=0$ (see condition 1.40). We impose continuity of solution and its derivative in the point $R$:

$$\left\{ {\begin{array}{lll} A\mathop{\rm sh}\nolimits ({\cal K}R)... ...thop{\rm ch}\nolimits ({\cal K}R) &=& Bk\cos(kR+\delta)\\ \end{array}} \right.$$ (1.56)

Condition of the continuity of the logarithmic derivative ${\cal K}\mathop{\rm cth}\nolimits ({\cal K}R)= k\mathop{\rm ctg}\nolimits (kR+\delta)$ fixes the phase $\delta(k)$ of the solution:

$$\delta(k) = \mathop{\rm arctg}\nolimits \left(\frac{k}{{\cal K}}\th{\cal K}R\right)-kR$$ (1.57)

This defines the relation between constants $A$ and $B$:

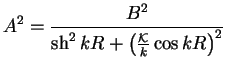$$A^2 = \frac{B^2}{\mathop{\rm sh}\nolimits ^2 kR+\left(\frac{{\cal K}}{k}\cos kR\right)^2}$$ (1.58)

By taking limit of low energy in (1.57) and using the definition (1.44) one obtains the expression for the $s$-wave scattering length for the scattering on the SS potential:

$$a_{3D} = R\left[1-\frac{\th\varkappa R}{\varkappa R}\right]$$ (1.59)

If in the case of the hard core potential (1.48) the potential energy is absent, it is no longer so here. This makes it reasonable to use a pair of potentials SS-HS in order to test the universality of the $s$-wave description (see, e.g., study done in Chapter. 3).