Many simplifications can be done in a homogeneous system due to the presence of the
translational symmetry. The correlation functions discussed above depend only on the
relative distance between two coordinates ![]() . The diagonal element of
. The diagonal element of ![]() is simply a constant
is simply a constant
![]() . The non-diagonal element of the normalized
one-body density matrix (in following we will address it as OBDM) is written as
. The non-diagonal element of the normalized
one-body density matrix (in following we will address it as OBDM) is written as
The normalized two-body density matrix (pair distribution function) is then given by
At the zero temperature some of the properties of the pair distribution can be
easily understood. At large distances the correlation between particles becomes
weaker and weaker and we can approximate the field operator
![]()
![]() and at zero temperature one has
and at zero temperature one has
![]() and
and ![]() approaches unity in the thermodynamic limit. On the
contrary at short distances particles ``feel'' each other and the value at zero can
be very different from the value in the bulk. In case of impenetrable particles, two
particles are not allowed to overlap, thus
approaches unity in the thermodynamic limit. On the
contrary at short distances particles ``feel'' each other and the value at zero can
be very different from the value in the bulk. In case of impenetrable particles, two
particles are not allowed to overlap, thus ![]() . For purely repulsive
interaction
. For purely repulsive
interaction ![]() and for purely attractive
and for purely attractive ![]() .
.
In the average of a two-body operator (1.8) it is possible to integrate out the
dummy variable and get a simple expression
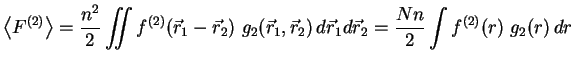 |
(1.20) |
For a particular case of a contact potential
![]() the
potential energy is directly related to the value of the pair distribution function
at zero:
the
potential energy is directly related to the value of the pair distribution function
at zero:
We will also give definition of the three-body density matrix1.2
Its value at zero gives the probability of finding three particles in the same point.