Momentum distribution and static structure factor

In terms of the field operator (1.1) the momentum distribution $n_k$ is given as

$$n_\k= \langle\hat\Psi^\dagger_\k\hat\Psi_\k\rangle,$$ (1.23)

The field operator in momentum space $\hat\Psi_\k$ is related to the $\hat\Psi(\r)$ by the Fourier transformation

$$\left\{ \begin{array}{lll} \hat\Psi_\k&= &\int e^{-i\k\r} \hat\Ps... ... &= &\int e^{i\k\r} \hat\Psi_\k\frac{d{\vec k}}{\sqrt{2\pi}} \end{array}\right.$$ (1.24)

Substitution of (1.24) into (1.23) gives following expression for the momentum distribution

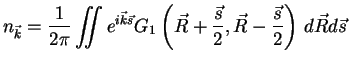$$n_\k= \frac{1}{2\pi} \int\!\!\!\!\int e^{i\k\vec s} G_1\left({\vec R}+\frac{\vec s}{2},\vec R-\frac{\vec s}{2}\right)\,d{\vec R}d\vec s$$ (1.25)

Note, that the dependence on $\k$ enters through the relative distance, so the center of the mass motion can be integrated out independently of $\k$. This procedure is used in the DMC (see Sec.2.7). In the homogeneous system one has

$$n_k = n\int e^{ikr} g_1(r)\,dr$$ (1.26)

At zero temperature the dynamic structure factor $S(k,\omega)$ is related to the $\k$-component of the density operator

$$\rho_k = \langle \hat\Psi^\dagger(r)\Psi(r)\rangle= \int e^{-ikr}n(r)\,dr$$ (1.27)

in the following way

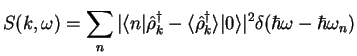$$S(k,\omega) = \sum\limits_n \vert\langle n \vert\hat\rho^\dagger_... ...le\hat\rho^\dagger_k\rangle\vert\rangle\vert^2\delta(\hbar\omega-\hbar\omega_n)$$ (1.28)

It characterizes the scattering cross-section of inelastic reactions where the scattering probe transfers momentum $\hbar k$ and energy $\hbar\omega$ to the system. By integrating out the $\omega$ dependence we obtain the static structure factor

$$S(k) = \frac{\hbar}{N} \int_0^\infty S(k,\omega)\,d\omega =\frac{1}{N}(\langle\rho_k\rho_{-k}\rangle - \vert\langle\rho_k\rangle\vert^2)$$ (1.29)

This expression is used in QMC calculations (refer to Sec. 2.7.2). Another useful representation can be obtained from Eqs. (1.10,1.27) and commutation relations for the field operator $\hat\Psi(\r)$. It relates the static structure factor to the two-body density matrix

$$S(k) = 1+\frac{1}{N} \int\!\!\!\!\int e^{ik(r_2-r_1)}(G_2(r_1,r_2)-n(r_1)n(r_2))\,dr_1dr_2$$ (1.30)

In a homogeneous system the two-body density matrix depends only on the relative distance $r = r_1-r_2$ and the static structure factor $S(r)$ is directly related to the pair distribution function (1.12)

$$S(k) = 1 + n\int e^{ikr} (g_2(r)-1)\,dr$$ (1.31)