



Next: Total energy
Up: Three-dimensional system
Previous: Three-dimensional system
Contents
Perturbed solution
We start from the three-dimensional energy functional (1.110) of a homogeneous
weakly-interacting Bose gas in the presence of a 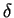 -function perturbation (an
impurity) moving with a constant velocity
-function perturbation (an
impurity) moving with a constant velocity 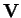
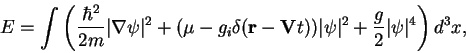 |
(7.1) |
where 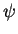 is the condensate wave function,
is the condensate wave function, 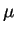 is the chemical potential,
is the chemical potential, 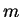 mass of a particle in the condensate,
mass of a particle in the condensate,
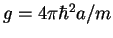 and
and
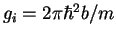 are particle-particle and particle-impurity coupling constants, with
are particle-particle and particle-impurity coupling constants, with 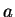 and
and 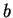 being the respective scattering lengths7.1. We will assume that the
interaction with impurity is small and we will use perturbation theory. By splitting
the wave function into a sum of the unperturbed solution and a small correction
being the respective scattering lengths7.1. We will assume that the
interaction with impurity is small and we will use perturbation theory. By splitting
the wave function into a sum of the unperturbed solution and a small correction
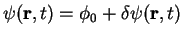 and linearizing the time-dependent GP equation
with respect to
and linearizing the time-dependent GP equation
with respect to 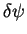 , we obtain an equation describing the time
evolution of
, we obtain an equation describing the time
evolution of 
 |
|
|
(7.2) |
In a homogeneous system  is a constant fixed by the particle density
is a constant fixed by the particle density
 and
and 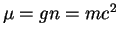 .
.
The perturbation follows the moving impurity, i.e. 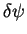 is a function of
is a function of
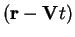 , so the coordinate derivative is related to
the time derivative
, so the coordinate derivative is related to
the time derivative
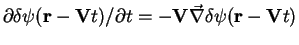 |
|
|
(7.3) |
We shall work in the frame moving with the impurity
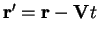 and the subscript over
and the subscript over 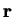 will be dropped.
will be dropped.
Eq. (7.2) for a perturbation in a homogeneous system can be
conveniently solved in momentum space. In order to do this we introduce the
Fourier transform of the wave function
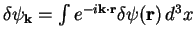 . Eq. (7.2
) becomes
. Eq. (7.2
) becomes
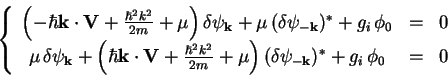 |
(7.4) |
Here the second equation is obtained by doing the substitution
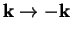 and and complex conjugation. We also use property of the Fourier
transformation
and and complex conjugation. We also use property of the Fourier
transformation
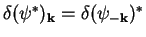 . The system
of linear equations (7.4) can be easily solved
. The system
of linear equations (7.4) can be easily solved
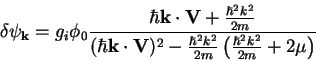 |
(7.5) |




Next: Total energy
Up: Three-dimensional system
Previous: Three-dimensional system
Contents
G.E. Astrakharchik
15-th of December 2004
![]() -function perturbation (an
impurity) moving with a constant velocity
-function perturbation (an
impurity) moving with a constant velocity ![]()
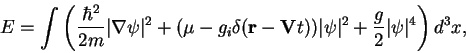
![]() is a constant fixed by the particle density
is a constant fixed by the particle density
![]() and
and ![]() .
.
![]() is a function of
is a function of
![]() , so the coordinate derivative is related to
the time derivative
, so the coordinate derivative is related to
the time derivative
![]() and the subscript over
and the subscript over ![]() will be dropped.
will be dropped.
![]() . Eq. (7.2
) becomes
. Eq. (7.2
) becomes