For a fixed value of the chemical potential ![]() the energy
the energy ![]() reaches
minimum on the ground state function
reaches
minimum on the ground state function ![]() . From this it follows that
. From this it follows that ![]() does
not have terms linear in
does
not have terms linear in
![]() and
and
![]() , and
, and
![$\displaystyle 2 E^{(2)} =
\int \left[
\delta \psi({\bf r}) \frac{\delta E^{(2)}...
...({\bf r}) \frac{\delta E^{(2)}}{\delta(\delta
\psi^*({\bf r}))}
\right]{\bf dr}$](img1502.gif) |
(7.7) |
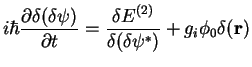 |
(7.8) |
To start with, let us Fourier transform the first term. Exchanging time derivatives
with gradients by the rule (7.3) one obtains
In the energy calculation we assume that the velocity ![]() is small and will make an
expansion in powers of
is small and will make an
expansion in powers of ![]() up to quadratic terms. It means that in the calculation
of
up to quadratic terms. It means that in the calculation
of
![]() the term
the term
![]() in the denominator of
(7.5) can be neglected and
in the denominator of
(7.5) can be neglected and
![]() is written as
is written as
The energy does not have terms linear in ![]() , because all terms independent of
, because all terms independent of
![]() in (7.11) are even in
in (7.11) are even in ![]() , so once multiplied by
, so once multiplied by ![]() and integrated over momentum space they provide zero contribution to the energy. The
only term that is left is the following
and integrated over momentum space they provide zero contribution to the energy. The
only term that is left is the following
For the calculation of ![]() in (7.6) and (7.9) one
should consider
in (7.6) and (7.9) one
should consider
![]() taking into account that
taking into account that
![]() and then integrate it over the momentum space
and then integrate it over the momentum space
The integral of the second term over momentum space is equal to zero.
The third term suffers from large-![]() divergency and one should renormalize the
scattering amplitude. It is sufficient to express the coupling constant in the
divergency and one should renormalize the
scattering amplitude. It is sufficient to express the coupling constant in the
![]() term of eq. (7.10) in terms of the scattering amplitude
term of eq. (7.10) in terms of the scattering amplitude ![]() using
the second order Born approximation:
using
the second order Born approximation:
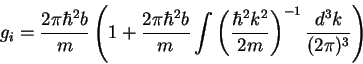 |
(7.14) |
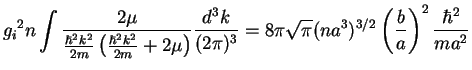 |
(7.15) |
The energy shift quadratic in velocity ![]() is defined by the following integral
is defined by the following integral
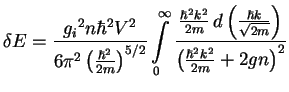 |
(7.17) |
This integral can be easily calculated if one recall the integral identity
![]() . Finally, by collecting everything together
and considering
. Finally, by collecting everything together
and considering ![]() impurities with a concentration given by
impurities with a concentration given by
![]() we obtain the energy per particle
we obtain the energy per particle
If we set ![]() we recover Bogoliubov's corrections to the energy in the presence of
quenched impurities [HM92,ABCG02]. Note that even if the ``mean-field''
energy obtained from the GP equation in the absence of impurities (
we recover Bogoliubov's corrections to the energy in the presence of
quenched impurities [HM92,ABCG02]. Note that even if the ``mean-field''
energy obtained from the GP equation in the absence of impurities (![]() ) leaves
out terms of the order of
) leaves
out terms of the order of ![]() , the equations we obtain in the presence of
impurities in a perturbative manner still correctly describe the effect of the
disorder up to the terms of the order of
, the equations we obtain in the presence of
impurities in a perturbative manner still correctly describe the effect of the
disorder up to the terms of the order of ![]() .
.