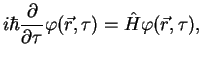 |
(2.6) |
The evolution of a quantum system is described by the Schrödinger equation
The formal solution
![]() can be
expanded in eigenstate functions of the Hamiltonian
can be
expanded in eigenstate functions of the Hamiltonian
![]() ,
where we order the eigenumbers in an increasing order
,
where we order the eigenumbers in an increasing order
![]()
In the long time limit the wave function remains finite only if ![]() is equal to
is equal to
![]() . The ground state energy
. The ground state energy ![]() will be estimated in a different way
(Sec. 2.7.1), but the fact that its estimation used for the energy shift value
will be estimated in a different way
(Sec. 2.7.1), but the fact that its estimation used for the energy shift value
![]() leads to a stable normalization of
leads to a stable normalization of
![]() proves in a different way
that the estimator is correct (for the implementation see Eq. 2.34).
proves in a different way
that the estimator is correct (for the implementation see Eq. 2.34).
The Hamiltonian of a system of ![]() particles interacting via pair-wise potential
particles interacting via pair-wise potential
![]() and subjected to an external field
and subjected to an external field ![]() in a most general form can be
written as
in a most general form can be
written as
The Schrödinger equation (2.7) reads as2.2
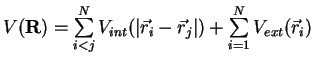 .
.
The efficiency of the method can be significantly improved if additional information
on the wave function is used. The idea is to
approximate the true wave function
![]() by a trial one
by a trial one
![]() and let
the algorithm correct the guess done. This approach is called
importance sampling and consists in solving the
Schrödinger equation for the modified wave function
and let
the algorithm correct the guess done. This approach is called
importance sampling and consists in solving the
Schrödinger equation for the modified wave function
Another reason for using the product of wave functions as the probability
distribution instead of sampling ![]() is that the average over the latter is ill
defined
is that the average over the latter is ill
defined
![]() , on the contrary the
average over the product of wave functions has the meaning of the mixed estimator
, on the contrary the
average over the product of wave functions has the meaning of the mixed estimator
![]() . From (2.11) it follows that
the distribution function
. From (2.11) it follows that
the distribution function ![]() satisfies the equation
satisfies the equation
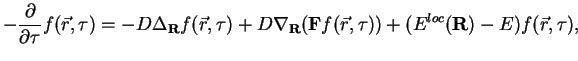 |
(2.13) |