Local energy

The most general form of a Hamiltonian of a system of $N$ interacting bosons in an external field is (2.10):

$$\hat H = -\frac{\hbar^2}{2m}\sum\limits_{i=1}^N \Delta_{{\vec r}_... ...}({\vec r}_i) + \sum\limits_{j<k}^N V_{int}(\vert{{\vec r}_j-{\vec r}_k}\vert),$$ (2.122)

where $m$ is mass of a particle, $V_{ext}({\vec r})$ is the external field, $V_{int}(\vert\r\vert)$ is particle-particle interaction potential. Given the many-body wave function $\Psi({{\vec r_1},...,{\vec r}_N})$ the local energy is defined according to (2.14):

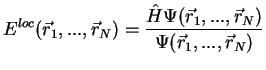$$E^{loc}({{\vec r_1},...,{\vec r}_N}) = \frac{\hat H \Psi({{\vec r_1},...,{\vec r}_N})}{\Psi({{\vec r_1},...,{\vec r}_N})}$$ (2.123)

Operator of the external field and particle-particle interaction are diagonal in this representation and are calculated trivially as a summation over particles and pairs of the second and third terms of (2.122). Calculation of the kinetic energy, first term of (2.122) is more tricky, as the Laplacian operator is not diagonal.