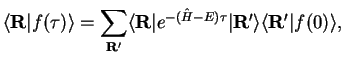 |
(2.16) |
The formal solution of the Schrödinger equation written in coordinate space is
given by
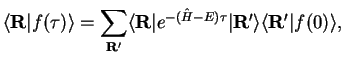 |
(2.16) |
In other words, the differential Schrödinger equation (2.6)
corresponds to the integral equation (2.17), which can be integrated with
help of Monte Carlo methods. Although the Green's function
![]() is not
known, it can be approximated at small times
is not
known, it can be approximated at small times ![]() , and then equation (2.17)
can be solved step by step
, and then equation (2.17)
can be solved step by step
The asymptotic solution for large times can be obtained by propagating
![]() for a large number
of time steps
for a large number
of time steps ![]() .
.
For further convenience let us split the Hamiltonian into three pieces
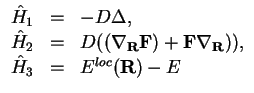 |
(2.21) |
Let us introduce the corresponding Green's functions:
The exponent of a sum of two operators (on the contrary to an exponent of
![]() -numbers) in general can not be written as a product of two exponents. The exact
relation takes into account the non-commutativity
-numbers) in general can not be written as a product of two exponents. The exact
relation takes into account the non-commutativity
![]() . The primitive
approximation consists in neglecting the noncommutativity
. The primitive
approximation consists in neglecting the noncommutativity
This formula, rewritten in the coordinate representation, gives the expression for
the Green's function
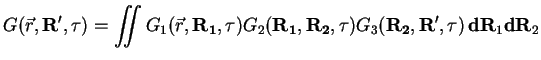 |
From Eq. 2.22 we find that the Green's function should satisfy Bloch
differential equation:
The equation for the kinetic term has the form
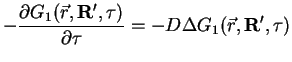 |
(2.25) |
This is the diffusion equation with diffusion constant
![]() . It can be
conveniently solved in a momentum representation where the kinetic energy operator
is diagonal. Going back to the coordinate representation one finds that the solution
is a Gaussian
. It can be
conveniently solved in a momentum representation where the kinetic energy operator
is diagonal. Going back to the coordinate representation one finds that the solution
is a Gaussian
The equation for the drift force term is
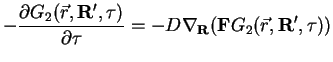 |
(2.27) |
The last equation from (2.24) has a trivial solution, which describes the branching term