We calculated the pair distribution matrix for a number of densities ranging from
very small value of the gas parameter
![]() (TG regime) up large
densities
(TG regime) up large
densities
![]() (GP regime). The results are presented in the
Fig. 5.3. In the GP regime the correlations between particles are very weak
and
(GP regime). The results are presented in the
Fig. 5.3. In the GP regime the correlations between particles are very weak
and ![]() arrives very quickly at the bulk value. Decreasing the
arrives very quickly at the bulk value. Decreasing the ![]() (thus
making the coupling constant
(thus
making the coupling constant ![]() larger) we enhance beyond-mean field effects
and enforce correlations. For the smallest considered value of the gas parameter
larger) we enhance beyond-mean field effects
and enforce correlations. For the smallest considered value of the gas parameter
![]() we see oscillations in the pair distribution function,
which, in this sense becomes more similar to the one of a liquid, rather than of a
gas. At the same density we compare the pair distribution function with the one of
the TG gas and find no visible difference.
we see oscillations in the pair distribution function,
which, in this sense becomes more similar to the one of a liquid, rather than of a
gas. At the same density we compare the pair distribution function with the one of
the TG gas and find no visible difference.
![\includegraphics[width=0.6\columnwidth]{LLg2.eps}](LLg2.gif)
|
On the same Figure we plot predictions for the value of the pair distribution
function at zero and find perfect agreement with the analytical prediction. In the
TG regime particles never meet each other and consequently ![]() . Making the
interaction between the particles weaker we find finite probability of two particles
coming close to each other according to the Eq. 5.10. As we go further
into the direction of the GP the interaction potential becomes more transparent and
we approach the ideal gas limit
. Making the
interaction between the particles weaker we find finite probability of two particles
coming close to each other according to the Eq. 5.10. As we go further
into the direction of the GP the interaction potential becomes more transparent and
we approach the ideal gas limit ![]() .
.
In the Fig. 5.4 we present the static structure factor obtained from
![]() according to relation (1.31). At the smallest density
according to relation (1.31). At the smallest density
![]() our points lie exactly on the top of the
our points lie exactly on the top of the ![]() of the TG
gas (Eq. 5.5). For all densities the small-momenta part of the structure
factor comes from generation of a phonon. We compare DMC results with the Feynman
prediction (Eq. 5.9). We see that in the strongly correlated regime
phononic description works well even to values of the momenta of the order of
inverse density
of the TG
gas (Eq. 5.5). For all densities the small-momenta part of the structure
factor comes from generation of a phonon. We compare DMC results with the Feynman
prediction (Eq. 5.9). We see that in the strongly correlated regime
phononic description works well even to values of the momenta of the order of
inverse density ![]() , although in the MF regime the healing length becomes
significantly larger than the mean interparticle distance leading to earlier
deviations.
, although in the MF regime the healing length becomes
significantly larger than the mean interparticle distance leading to earlier
deviations.
![\includegraphics[width=0.6\columnwidth]{LLSk.eps}](LLSk.gif)
|
We calculate the value at zero of the three-body correlation function (1.22)
over a large range of densities. At large density
![]() the
probability of three-body collisions is high. Making the density smaller we find
decrease in the value of
the
probability of three-body collisions is high. Making the density smaller we find
decrease in the value of ![]() . Close to the MF limit the result of the
Bogoliubov theory (Eq. 5.13) provides fairly good description of
. Close to the MF limit the result of the
Bogoliubov theory (Eq. 5.13) provides fairly good description of ![]() (see. Fig. 5.5). Further decrease in the density leads to fast decay of
three-body collision rate and it becomes vanishing at values of the gas parameter
smaller than one. In order to resolve the law of the decay we plot same data on the
log-log scale (Fig. 5.6) and show that the decay goes with the forth
power of the gas parameter in agreement with Eq. 5.12. Numerical estimation
of
(see. Fig. 5.5). Further decrease in the density leads to fast decay of
three-body collision rate and it becomes vanishing at values of the gas parameter
smaller than one. In order to resolve the law of the decay we plot same data on the
log-log scale (Fig. 5.6) and show that the decay goes with the forth
power of the gas parameter in agreement with Eq. 5.12. Numerical estimation
of ![]() at smaller densities becomes very difficult due to very small value of
the measured quantity itself. It is interesting to note that
at smaller densities becomes very difficult due to very small value of
the measured quantity itself. It is interesting to note that ![]() follows
closely to
follows
closely to ![]() .
.
We compare the result of an experiment done in NIST [TOH+04] with the
theoretical prediction of the Lieb-Liniger model, see
Figs. 5.5,5.6.
In this experiment the three body recombination rate was measured and the
value of ![]() was extracted. We find an agreement between experiment and theory.
The result of DMC calculation is slightly closer to the experimental data point than
the estimation
was extracted. We find an agreement between experiment and theory.
The result of DMC calculation is slightly closer to the experimental data point than
the estimation ![]() , although the error bars of the experimental measurement
cover both values.
, although the error bars of the experimental measurement
cover both values.
![\includegraphics[width=0.6\columnwidth]{LLg3.eps}](LLg3.gif)
|
![\includegraphics[width=0.6\columnwidth]{LLg3log.eps}](LLg3log.gif)
|
We calculated the spatial dependence of the one-body density matrix for different
densities. At small distances we compare the function with the short range expansion
(5.14) and find an agreement for ![]() (see Fig. 5.7). For distances larger than the healing length we expect the hydrodynamic
theory to provide a correct description. Indeed, we see that the long-range decay
has a power-law form in agreement with the prediction Eq. 5.7 (see
Fig. 5.8). We fix the coefficient of proportionally in Eq. 5.7
by fitting the data. By doing it we conclude complete description of the one-body
density matrix starting from small distances up to large ones. The deviations on
Fig. 5.8 from power law-decay are at largest distances (
(see Fig. 5.7). For distances larger than the healing length we expect the hydrodynamic
theory to provide a correct description. Indeed, we see that the long-range decay
has a power-law form in agreement with the prediction Eq. 5.7 (see
Fig. 5.8). We fix the coefficient of proportionally in Eq. 5.7
by fitting the data. By doing it we conclude complete description of the one-body
density matrix starting from small distances up to large ones. The deviations on
Fig. 5.8 from power law-decay are at largest distances (![]() ) are
due to finite size effects.
) are
due to finite size effects.
We derive a highly accurate expression for the coefficient ![]() from a
hydrodynamic approach considering weak interactions and low density fluctuations. In
terms of Euler's constant
from a
hydrodynamic approach considering weak interactions and low density fluctuations. In
terms of Euler's constant ![]() we have (1.199):
we have (1.199):
Although this constant is formally derived in the limit ![]() (i.e. limit of
weak interaction
(i.e. limit of
weak interaction
![]() ) it provides a very good description in the
whole range of densities. Indeed, the coefficient defined by fitting
) it provides a very good description in the
whole range of densities. Indeed, the coefficient defined by fitting ![]() as
shown in Fig. 5.8 is always in agreement with prediction (5.15)
within the uncertainty errorbars we get from our DMC calculation. Further, in the
most strongly interacting TG regime we compare (5.15) with the exact result
provided by formula (5.6) and find only
as
shown in Fig. 5.8 is always in agreement with prediction (5.15)
within the uncertainty errorbars we get from our DMC calculation. Further, in the
most strongly interacting TG regime we compare (5.15) with the exact result
provided by formula (5.6) and find only ![]() difference.
A different expression was obtained by Popov [Pop80] (and later recovered in
[MC02])
difference.
A different expression was obtained by Popov [Pop80] (and later recovered in
[MC02])
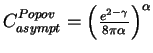 . Both expressions coincide for
small values of
. Both expressions coincide for
small values of ![]() , but Popov's coefficient lead up to larger
, but Popov's coefficient lead up to larger ![]() maximal
error, as it was pointed out in [Caz04]. The comparison of different
coefficients is presented in Table 5.2.
maximal
error, as it was pointed out in [Caz04]. The comparison of different
coefficients is presented in Table 5.2.
![\includegraphics[width=0.6\columnwidth]{LLg1small.eps}](LLg1small.gif)
|
![\includegraphics[width=0.6\columnwidth]{LLg1.eps}](LLg1.gif)
|
We obtain the momentum distribution from the Fourier transformation (see
Eq. 1.26) of the one-body density matrix at short distances and the fit
power-law decay at large distances. In an infinite homogeneous system the momentum
distribution has an infrared divergence (Eq. 5.8). In order to present
the momentum distribution in the most efficient way we plot in Fig. 5.9 a
combination ![]() , where this divergence is absent. We notice that the infrared
asymptotic behavior is recovered for values of
, where this divergence is absent. We notice that the infrared
asymptotic behavior is recovered for values of ![]() considerably smaller than the
inverse healing length
considerably smaller than the
inverse healing length ![]() . At large
. At large ![]() the numerical noise of our results is
too large to extract evidences of
the numerical noise of our results is
too large to extract evidences of ![]() behavior predicted in [OD03].
behavior predicted in [OD03].
![\includegraphics[width=0.6\columnwidth]{LLnk.eps}](LLnk.gif)
|