We use Diffusion Monte Carlo (DMC) technique in order to obtain the ground state
properties of the system.
A good choice of the trial wave-function is crucial for the efficiency of the
calculation. In order to prove that our trial wave-function is indeed very close to
the true ground state wave function we perform calculation of the variational energy
![]() which provides an upper-bound to the ground state energy (see
Table 5.1). We find that the variational energy is at maximum
which provides an upper-bound to the ground state energy (see
Table 5.1). We find that the variational energy is at maximum ![]() higher than the energy of the DMC calculation, which coincides with the exact
solution based on the use of the Bethe ansatz (see, also, Fig. 5.1).
higher than the energy of the DMC calculation, which coincides with the exact
solution based on the use of the Bethe ansatz (see, also, Fig. 5.1).
In a homogeneous system we use the Bijl-Jastrow construction (2.37) of the
trial wave function. The construction of the two-body term ![]() is described
in Sec. 2.5.4.5. The
is described
in Sec. 2.5.4.5. The ![]() part corresponds to the exact solution of the
two-body problem and provides a correct description of short-range correlations.
Long-range correlations arising from phonon excitations are instead accounted for by
the functional dependence of
part corresponds to the exact solution of the
two-body problem and provides a correct description of short-range correlations.
Long-range correlations arising from phonon excitations are instead accounted for by
the functional dependence of ![]() for
for ![]() [RC67].
The value of the matching point
[RC67].
The value of the matching point ![]() is a variational parameter which we optimize
using the variational Monte Carlo (VMC). The TG wave function (2.5.4.1) is
obtained as a special case of our trial wave function (2.55) for
is a variational parameter which we optimize
using the variational Monte Carlo (VMC). The TG wave function (2.5.4.1) is
obtained as a special case of our trial wave function (2.55) for ![]() and
and ![]() .
.
The level of accuracy of the trial wave function is particularly important for the
calculation of the of ![]() . Instead, the pair distribution function
. Instead, the pair distribution function ![]() is
calculated using the method of ``pure'' estimators, unbiased by the choice of the
trial wave function [CB95]. Due to non local property of the one-body
density matrix, the function
is
calculated using the method of ``pure'' estimators, unbiased by the choice of the
trial wave function [CB95]. Due to non local property of the one-body
density matrix, the function ![]() can instead by obtained only through the
extrapolation technique. For an operator
can instead by obtained only through the
extrapolation technique. For an operator ![]() , which does not commute with the
Hamiltonian, the output of the DMC method is a ``mixed'' estimator
, which does not commute with the
Hamiltonian, the output of the DMC method is a ``mixed'' estimator
![]() . Combined together with the variational
estimator
. Combined together with the variational
estimator
![]() obtained from the VMC calculation it
can be used for extrapolation to the ``pure'' estimator by the rule
obtained from the VMC calculation it
can be used for extrapolation to the ``pure'' estimator by the rule
![]() . Of course, this procedure is
very accurate only if
. Of course, this procedure is
very accurate only if
![]() . We find that DMC and VMC give results for
. We find that DMC and VMC give results for ![]() which are very close and
we believe that the extrapolation technique is in this case exact.
which are very close and
we believe that the extrapolation technique is in this case exact.
We consider ![]() particles in a box of size
particles in a box of size ![]() with periodic boundary conditions. In
the construction of the trial wave function we have ensured that the two-body term
with periodic boundary conditions. In
the construction of the trial wave function we have ensured that the two-body term
![]() is uncorrelated at the boundaries
is uncorrelated at the boundaries
![]() . In order to estimate
properties of an infinite system we we increase number of particles and study
convergence in the quantities of interest. The dependence on the number of particles
(finite size effects) are more pronounced at the large density where the
correlations extend up to large distances. Out of the quantities we measured, the
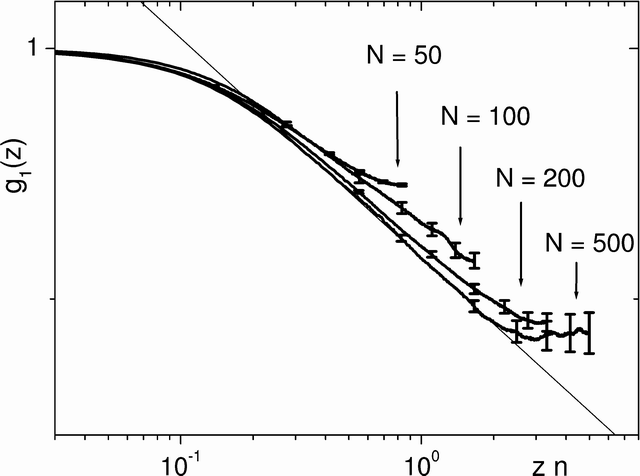
one-body density matrix is the most sensitive to finite size corrections. As an
example in Fig. 5.2 we show
. In order to estimate
properties of an infinite system we we increase number of particles and study
convergence in the quantities of interest. The dependence on the number of particles
(finite size effects) are more pronounced at the large density where the
correlations extend up to large distances. Out of the quantities we measured, the
one-body density matrix is the most sensitive to finite size corrections. As an
example in Fig. 5.2 we show ![]() at density
at density
![]() for 50, 100, 200 and 500 particles and make comparison it with the asymptotic
for 50, 100, 200 and 500 particles and make comparison it with the asymptotic
![]() behavior. We find largest finite size effects near the maximal distance
behavior. We find largest finite size effects near the maximal distance
![]() for which the one-body density matrix can be calculated. Also we see a
dependence of the slope on the number of particles. Already for 500 particles we
find the correct slope of the one-body density matrix. For the smaller densities,
where finite size effects are smaller, it is sufficient to have
for which the one-body density matrix can be calculated. Also we see a
dependence of the slope on the number of particles. Already for 500 particles we
find the correct slope of the one-body density matrix. For the smaller densities,
where finite size effects are smaller, it is sufficient to have ![]() .
.
|