Phonon trial wave function (
Here we shall construct a trial wave function which at distances short is a two-body
solution of one-dimensional ![]() -function scattering and has ``phonon'' like
behavior at large distances (see [RC67]).
-function scattering and has ``phonon'' like
behavior at large distances (see [RC67]).
The trial wave function is chosen in the following form
There are five undefined parameters
![]() and four continuity equations.
One parameter is left free. We will chose matching distance
and four continuity equations.
One parameter is left free. We will chose matching distance ![]() as the guiding
parameter.
as the guiding
parameter.
| (2.56) |
This equation fixes the value of the scattering momenta ![]() .
.
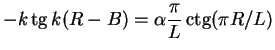 |
(2.58) |
![$\displaystyle -k^2 = \alpha
\left(\frac{\pi}{L}\right)^2 [(\alpha-1)\mathop{\rm ctg}\nolimits ^2(\pi R/L)-1]$](img870.gif) |
(2.59) |
One can prove that following relation holds
![]() . Another useful relation is
. Another useful relation is
![]() .
.
The value of the scattering momenta is a solution of the equation
The maximal value of the l.h.s. is reached at ![]() and equals to
and equals to ![]() . For
matching distance much smaller than
. For
matching distance much smaller than ![]() the sinus function on the r.h.s. can be
expanded and the condition for the existence of the solution is
the sinus function on the r.h.s. can be
expanded and the condition for the existence of the solution is ![]() which is
always fulfilled for the repulsive gas.
which is
always fulfilled for the repulsive gas.
All other parameters can be found from the following formulae:
The contribution to the energy is given by
![$\displaystyle -\frac{f''}{f}+\left(\frac{f'}{f}\right)^2 =
\left\{
{\begin{arra...
...hop{\rm ctg}\nolimits ^2 \frac{\pi x}{L}\right], & z \ge R
\end{array}}
\right.$](img877.gif) |
(2.62) |