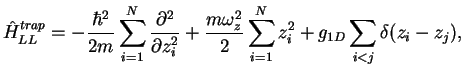 |
(5.16) |
Now let us consider effects of the external trap. We consider the trapping potential
to be a harmonic oscillator. The effective one-dimensional Hamiltonian is then given
by
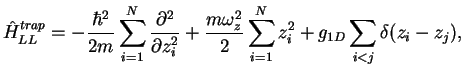 |
(5.16) |
In the construction of the trial wave function used in our DMC calculation we
introduce one-body Jastrow term ![]() in addition to the two-body terms
in addition to the two-body terms
![]() already contained in homogeneous trial wave function (2.55).
Taking into account the harmonic nature of the external potential we choose the
one-body term in the Gaussian form
already contained in homogeneous trial wave function (2.55).
Taking into account the harmonic nature of the external potential we choose the
one-body term in the Gaussian form
![]() with
with ![]() being the variational parameter. The correlations at distances much larger than the
longitudinal oscillator length
being the variational parameter. The correlations at distances much larger than the
longitudinal oscillator length
![]() are dominated by the
oscillator confinement and two-body correlations become irrelevant.
are dominated by the
oscillator confinement and two-body correlations become irrelevant.
We consider the following configurations:
![]() ,
,
![]() and
number of particles
and
number of particles
![]() . In Sec. 3 we have proven
that in these conditions the ground-state energy and structure of the cloud is
correctly described by the Lieb-Liniger equation of state in local density
approximation.
. In Sec. 3 we have proven
that in these conditions the ground-state energy and structure of the cloud is
correctly described by the Lieb-Liniger equation of state in local density
approximation.
In Fig. 5.10 we plot the pair distribution function (2.146) for 5, 20 and 100 particles. The short-range dependence is dominated by two-body interactions. We do not find oscillations which means that strong shell structure is absent. At large distances the external trapping suppresses density.
We refer to general definition of the static structure factor in terms of the
momentum distribution ![]() (2.133):
(2.133):
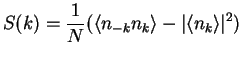 |
(5.17) |
On the contrary uniform case, the last term is no longer vanishing for ![]() in a
trap. In Fig. 5.11 we present the static structure factor obtained for
the same set of parameters. We are interested in evidences of the linear behavior
characteristic for the phonon propagation. We discover that Feynmann formula
(5.9) with the speed of sound taken at the center of the trap provides
relatively good description also for the trapped systems. Of course, the very low
momenta part is different due to the finite size effects.
in a
trap. In Fig. 5.11 we present the static structure factor obtained for
the same set of parameters. We are interested in evidences of the linear behavior
characteristic for the phonon propagation. We discover that Feynmann formula
(5.9) with the speed of sound taken at the center of the trap provides
relatively good description also for the trapped systems. Of course, the very low
momenta part is different due to the finite size effects.
For the smallest number of particles considered (![]() ), the density is always small
), the density is always small
![]() and we can derive an explicit expression for the
and we can derive an explicit expression for the ![]() exploiting knowledge of the static structure factor in the limit of small density
(5.5) as explained in Sec. 1.6.4. The resulting expression is
given by formula (1.154). an be calculated.
We find that thr linear behavior at small
exploiting knowledge of the static structure factor in the limit of small density
(5.5) as explained in Sec. 1.6.4. The resulting expression is
given by formula (1.154). an be calculated.
We find that thr linear behavior at small ![]() matches the asymptotic constant in a
smoother way than it happens in a homogeneous system (see TG static structure factor
in Fig. 5.4).
matches the asymptotic constant in a
smoother way than it happens in a homogeneous system (see TG static structure factor
in Fig. 5.4).
|
|
In Fig. 5.12 we show the results for the momentum distribution ![]() .
On the contrary to homogeneous case,
.
On the contrary to homogeneous case, ![]() in a finite system always remain finite
due to natural limitations on the minimal possible value of wave vector
in a finite system always remain finite
due to natural limitations on the minimal possible value of wave vector
![]() , where
, where ![]() is the size of the cloud in the axial direction. We are
looking for traces of the divergent behavior at small momenta similar to (5.8). In the case of
is the size of the cloud in the axial direction. We are
looking for traces of the divergent behavior at small momenta similar to (5.8). In the case of ![]() and
and ![]() the rounding off of
the rounding off of ![]() at
at ![]() washes out completely the divergent behavior. For the largest system with
washes out completely the divergent behavior. For the largest system with
![]() we find some evidence of the infrared behavior (see inset in Fig. 5.12) in the region of wave vectors
we find some evidence of the infrared behavior (see inset in Fig. 5.12) in the region of wave vectors
![]() . The healing length is
estimated by the density in the center of the trap
. The healing length is
estimated by the density in the center of the trap
![]() . We also
plot a power law function with the exponent
. We also
plot a power law function with the exponent
![]() which corresponds
to the value in a homogeneous system with same density and the coefficient of
proportionality obtained by best fit. In order to see a cleaner signature of the
infrared behavior one should consider much larger systems.
which corresponds
to the value in a homogeneous system with same density and the coefficient of
proportionality obtained by best fit. In order to see a cleaner signature of the
infrared behavior one should consider much larger systems.
|
|