Soluzione di alcuni degli esercizi proposti

Soluzione dell'esercizio 1.1  

    

Soluzione dell'esercizio 1.2  

    

Soluzione dell'esercizio 1.3  

    

Soluzione dell'esercizio 1.4  

    

Soluzione dell'esercizio 1.5  

    

Soluzione dell'esercizio 1.6  

    

Soluzione dell'esercizio 1.7  

    

Soluzione dell'esercizio 1.8  

    

Soluzione dell'esercizio 1.9  

    

Soluzione dell'esercizio 1.10  Siano $f:X\to I_n$ e $g : Y \to I_n$ due bigezioni, allora l'applicazione $h:I_{n+m}\to X\cup Y$ definita da

$$h(i)=\Big\langle \begin{array}{lcl} f(i) &&\hbox{\rm {se }} i<n \\ g(i-n) && \hbox{\rm {se }} n\le i < m+n \end{array}$$

è una bigezione.

Per la seconda parte si osservi innanzitutto che $X= (X-Y)\cup (X\cap Y)$ e che $(X-Y)\cap (X\cap Y)=\varnothing$ e che quindi per l'esercizio precedente,

$$\left\vert X\right\vert = \left\vert X-Y\right\vert + \left\vert X\cap Y\right\vert$$

osserviamo inoltre che $X\cup Y=(X-Y)\cup Y$ con $(X-Y)\cap Y=\varnothing$e quindi $\left\vert X\cup Y\right\vert= \left\vert X-Y\right\vert+ \left\vert Y\right\vert$, da cui

$$\left\vert Y\right\vert=\left\vert X\cup Y\right\vert - \left\vert X-Y\right\vert$$

sommando queste due relazioni si ottiene la tesi.     

Soluzione dell'esercizio 1.11  Procediamo per induzione su n. Se n=1 non c'è nulla da dimostrare. Supponiamo la tesi vera per n, usando l'associatività dell'unione si ha

$$\bigcup_{i=1}^{n+1} X_i= ( \bigcup_{i=1}^{n} X_i )\cup X_{n+1}$$

e dato che gli X_i sono a due a due disgiunti, anche $( \bigcup_{i=1}^{n} X_i )\cap X_{n+1}=\varnothing$, ma allora per l'esercizio precedente, e l'ipotesi di induzione, si ha che

$$\left\vert\bigcup_{i=1}^{n+1} X_i\right\vert= \left\vert\big... ...t X_{n+1}\right\vert=\sum_{i+1}^{n+1}\left\vert X_i\right\vert$$

    

Soluzione dell'esercizio 1.12  

    

Soluzione dell'esercizio 1.13  

    

Soluzione dell'esercizio 1.14  

    

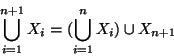
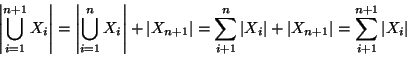
Soluzione dell'esercizio 2.1   Se una tale g esiste, f è surgettiva, dato che per ogni $y\in Y$si ha che f(g(y))=y.

Viceversa, supponiamo che f sia surgettiva, allora $f^{-1}(y)\ne\varnothing$ per ogni $y\in Y$, per l'assioma di scelta, esiste una funzione di scelta, $g:Y\to\bigcup_{y\in Y}f^{-1}(y)$, tale che $g(y)\in f^{-1}(y)$ per ogni $y\in Y$, ma ciò significa che f(g(y))=y per ogni $y\in Y$, ossia che g è una inversa destra di f.     

Soluzione dell'esercizio 2.2  Se una tale g esiste allora f deve necessariamente essere iniettiva, infatti se f(x₁)=f(x₂) allora x₁=g(f(x₁))=g(f(x₂))x₂.

Viceversa, supponiamo che f sia iniettiva. Allora per ogni $y\in f(X)$ esiste un unico $x_y\in X$ tale che f(x_y)=y. Preso un arbitrario $\overline{x}\in X$definiamo $g:Y\to X$ ponendo

$$g(y)=\Big\langle \begin{array}{lcl} x_y &&\hbox{\rm {se }}y... ...) \\ \overline{x} &&\hbox{\rm {se }}y\notin f(X) \end{array}$$

Dato che per ogni $x\in X$ l'unico elemento avente f(x) come immagine è x stesso, si ha che g(f(x))=x.     

Soluzione dell'esercizio 2.3  

    

Soluzione dell'esercizio 2.4  A partire dagli X_m costruiamo dei nuovi insiemi, ponendo

$$\begin{eqnarray*}Y_0 & = & X_0 \\ Y_{n+1} & = & X_{n+1} - \bigcup_{m=0}^{n} X_m \qquad \forall n \ge 0 \end{eqnarray*}$$

Gli insiemi in questione sono a due a due disgiunti, e $\bigcup_nY_n=\bigcup_nX_n$. Si consideri l'insieme $A=\{n\in\mathbb N\mid Y_n\ne\varnothing\}$, allora $Y=\bigcup_{n\in A}Y_n$. Per quanto visto in precedenza Aè finito o numerabile. Nel primo caso A è finito, nel secondo caso è numerabile.     

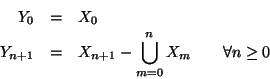
Soluzione dell'esercizio 2.5  Come nell'esercizio precedente, poniamo

$$\begin{eqnarray*}Y_0 & = & X_0 \\ Y_{n+1} & = & X_{n+1} - \bigcup_{m=0}^{n} X_m \qquad \forall n \ge 0 \end{eqnarray*}$$

Gli insiemi in questione sono a due a due disgiunti, e $\bigcup_nY_n=\bigcup_nX_n$. Si consideri l'insieme $A=\{n\in\mathbb N\mid \left\vert Y_n\right\vert=\aleph_0\}$, $B=\{n\in\mathbb N\mid Y_n\ne\varnothing\hbox{\rm { ed \\lq e finito}}\}$, allora $Y=\bigcup_{n\in A}Y_n\cup\bigcup_{n\in B}Y_n$. Per quanto visto in precedenza A, e B sono finiti o numerabili. Dato che Y₀ è numerabile, $A\ne\varnothing$e quindi $\bigcup_{n\in A}Y_n$ è numerabile. D'altra parte $\bigcup_{n\in B}Y_n$ è finito o numerabile e quindi la loro unione è numerabile.     

Soluzione dell'esercizio 2.6  

    

Soluzione dell'esercizio 3.1  

    

Soluzione dell'esercizio 3.2  

    

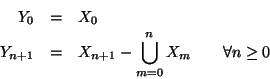
Soluzione dell'esercizio 3.3  La funzione $f:(0,1)\to\mathbb R$ definita da $f(t)=\tan(\pi t-\pi/2)$ è una bigezione.     

Soluzione dell'esercizio 3.4  Osserviamo che X-Y non può essere né finito né numerabile, altrimenti $X=(X-Y)\cup Y$ sarebbe numerabile. Ma allora X-Ycontiene un sottinsieme, Y', numerabile. Dato che Y e Y' sono entrambi numerabili, la loro unione è numerabile, sia quindi $f:Y'\to Y\cup Y'$ una bigezione e si definisca $g:X-Y\to X$ ponendo:

$$g(x)=\Big\langle \begin{array}{lcl} f(x) &&\hbox{\rm {se }} x\in Y' \\ x &&\hbox{\rm {se }} x\in X-(Y\cup Y') \end{array}$$

g è chiaramente una bigezione.     

Soluzione dell'esercizio 3.5  Per ogni $k\in \mathbb N$ sia $F_k=\{A\in 2^\mathbb N\mid \left\vert A\right\vert = k\}$. Chiaramente $F=\bigcup_{k\in\mathbb N}F_k$. Proviamo che $\left\vert F_k\right\vert=\aleph_0$ per ogni $k\ge1$. Procediamo per induzione su k. Se k=1 allora l'applicazione $n\to \{n\}$è una bigezione $\mathbb N\to F_1$. Supponiamo che F_k sia numerabile, allora per ogni $A\in F_k$ sia $F_{k+1}(A)=\{B\in F_{k+1}\mid B\supseteq A\}$. per ogni Al'insieme F_k+1(A) è numerabile, in quanto in bigezione con $\mathbb N-A$, inoltre $F_{k+1}-\bigcup_{A\in F_k}F_{k+1}(A)$ è numerabile in quanto unione di una famiglia numerabile di insiemi numerabili.     

Soluzione dell'esercizio 3.6  

    

Soluzione dell'esercizio 3.7  

    

Soluzione dell'esercizio 3.8  

    

Soluzione dell'esercizio 3.9  

    

Soluzione dell'esercizio 3.10  

    

Soluzione dell'esercizio 4.1  

    

Soluzione dell'esercizio 4.2  

    

Soluzione dell'esercizio 4.3  

    

Soluzione dell'esercizio 5.1  

    

Soluzione dell'esercizio 5.2  

    

Soluzione dell'esercizio 5.3  Si osservi che se X è un insieme con n elementi, allora

$$2^X=\bigcup_{i=0}^n{X \choose k}$$

e che questi insiemi sono a due a due disgiunti. Quindi

$$2^n=2^{\left\vert X\right\vert}=\left\vert 2^X\right\vert=\su... ...n{\left\vert X\right\vert \choose k}=\sum_{i=0}^n{n \choose k}$$

    

Soluzione dell'esercizio 5.4  

    

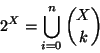
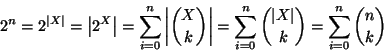
Soluzione dell'esercizio 6.1  Procediamo per induzione su k. Se k=1 non c'è nulla da dimostrare. Supponiamo che la tesi sia vera per k e supponiamo che $p\mathrel{\big\vert}n_1n_2\dots n_{k+1}$, ossia $p\mathrel{\big\vert}(n_1n_2\dots n_k)n_{k+1}$. Per il corollario 6.3, si ha che $p\mathrel{\big\vert} n_1n_2\dots n_k$ oppure $p\mathrel{\big\vert}n_{k+1}$. Se si verifica la seconda eventualità abbiamo finito, altrimenti, per ipotesi di induzione esiste $i\in \{1,\dots,k\}$ tale che $p\mathrel{\big\vert}n_i$, e quindi si conclude.     

Soluzione dell'esercizio 6.2  

    

Soluzione dell'esercizio 6.3  

    

Soluzione dell'esercizio 6.4  Chiaramente $\prod _{i=1}^s p_i^{k_i\wedge h_i}$ è un divisore comune a n e m. Inoltre se c è un divisore comune non può avere fattori primi diversi dai p_i, quindi $c=\prod _{i=1}^s p_i^{l_i}$. Dal fatto che $c\mathrel{\big\vert}n$ segue allora che $l_i\le k_i$ e dal fatto che $c\mathrel{\big\vert}m$ segue che $l_i\le h_i$ per ogni i, e quindi $l_i\le k_i\wedge h_i$.

La formula per il m.c.m. segue allora dal fatto che $[n,m]=\left\vert nm\right\vert/(n,m)$, e che per ogni coppia di numeri reali si ha che $h+k-h\wedge k=h\vee k$.     

Soluzione dell'esercizio 7.1  

    

Soluzione dell'esercizio 7.2  

    

Soluzione dell'esercizio 7.3  

    

Soluzione dell'esercizio 7.4  

    

Soluzione dell'esercizio 8.1  

    

Soluzione dell'esercizio 8.2  

    

Soluzione dell'esercizio 8.3  

    

Soluzione dell'esercizio 8.4  

    

Soluzione dell'esercizio 9.1  

    

Soluzione dell'esercizio 9.2  Osserviamo che $(a,pq)\ne1$ se e solo se $p \mathrel{\big\vert}a$ o $p \mathrel{\big\vert}a$, ma i numeri più piccoli di pq che sono divisibili per p sono p, $2p,\dots,qp$, quelli che sono divisibili per q sono invece q, $2q,\dots,pq$ e quindi i numeri più piccoli di pq e non coprimi con pq sono p+q-1. Quindi $\Phi(pq)=pq-(p+q-1)=(p-1)(q-1)$.     

Soluzione dell'esercizio 9.3   $\Phi(n)=(p-1)(q-1)=pq -p -q +1= n -p -q +1$ da cui $p+q=n+1-\Phi(n)$. Quindi p e q sono determinati dal sistema di equazioni

$$\left\{ \begin{array}{l} p+q=n+1-\Phi(n) \\ pq=n \end{array} \right.$$

Una semplice sostituzione mostra che allora p e q devono essere le due radici dell'equazione $x^2-(n+1-\Phi(n))+n=0$.     

Soluzione dell'esercizio 9.4  

    

Soluzione dell'esercizio 10.1  

    

Soluzione dell'esercizio 14.1  

    

Soluzione dell'esercizio 14.2  

    

Soluzione dell'esercizio 14.3  

    

Soluzione dell'esercizio 14.4  

    

Soluzione dell'esercizio 14.5  La colorazione dei lati data in figura 13

  

Figure 13: Soluzione grafica dell'esercizio 14.5

suggerisce come definire l'isomorfismo. Precismante se si definisce la funzione $f:\{1,2,\dots,10\}\to\{a,b,\dots,j\}$ ponendo

$$\begin{array}{rclcrclcrclcrclcrcl} f(1)&=&a &\quad & f(2)&=&... ...d & f(8)&=&h &\quad & f(9)&=&i &\quad & f(10)&=&j \end{array}$$

una semplice verifica mostra che f è un isomorfismo.     

Soluzione dell'esercizio 14.6  

    

Soluzione dell'esercizio 14.7  

    

Soluzione dell'esercizio 14.8  Se identifichiamo la lettera a con il numero 0 e la b con l'1, si ottiene una identificazione delle parole con le coordinate dei vertici del cubo di $\mathbb R^3$ dato da $[0,1]\times[0,1]\times[0,1]$. Inoltre due vertici di tale cubo sono congiunti da uno spigolo se solo se differiscono esattamente per una coordinata. L'identificazione data è quindi un isomorfismo di grafi tra G e G'.

  

Figure 14: L'isomorfismo tra i grafi dell'esercizio 14.8

    

Soluzione dell'esercizio 18.1  

    

Soluzione dell'esercizio 18.2  

    

Soluzione dell'esercizio 18.3  

    

Soluzione dell'esercizio 18.4  

    

Soluzione dell'esercizio 18.5  

    

Soluzione dell'esercizio 18.6  

    

Soluzione dell'esercizio 18.7  

    

Soluzione dell'esercizio 19.1  

    

Soluzione dell'esercizio 19.3  

    

Soluzione dell'esercizio 19.4  

    

Soluzione dell'esercizio 19.5  

    

Soluzione dell'esercizio 19.6  

    

Soluzione dell'esercizio 19.7  Procediamo per induzione sul numero dei lati. Se $\left\vert E(G)\right\vert=0$ il grafo ha un solo vertice e quindi è lui stesso un albero.

Supponiamo che $\left\vert E(G)\right\vert\ge1$, allora s. Se per ogni $e\in E$, G-e è sconnesso, allora per la terza delle proprietà che caratterizzano gli alberi, si ha che G è un albero. Se invece esiste un e tale che G-e è connesso, allora, avendo un lato in meno di G, per ipotesi di induzione G-e ha un per sottografo un albero che contiene tutti i suoi vertici (e quindi tutti i vertici di G). Chiaramente questo sottografo è sottografo anche di G.     

Soluzione dell'esercizio 19.8  Sia T un albero generatore di G. Chiaramente $\left\vert V(T)\right\vert=\left\vert V(G)\right\vert$ e dato che T è un sottografo di G allora $\left\vert E(T)\right\vert\le \left\vert E(G)\right\vert$ e quindi, usando la formula che lega il numero di lati con il numero dei vertici di un grafo, si ha

$$\left\vert E(G)\right\vert\ge \left\vert E(T)\right\vert = \left\vert V(T)\right\vert - 1 = \left\vert V(G)\right\vert - 1.$$

    

Soluzione dell'esercizio 20.1  

    

Soluzione dell'esercizio 20.2  Si definisce passeggiata diretta una successione finita di vertici $(v_0,v_1,\dots,v_n)$ tali che $v_i\to v_{i+1}$ per ogni i. Una passeggiata diretta si dirà un cammino diretto se e solo se i vertici v₁ sono a due a due distinti, una passeggiata diretta si dirà un ciclo diretto se e solo se i vertici sono a due a due distinti a parte il primo e l'ultimo che coincidono.

Proviamo che se due vertici sono congiungibili da una passeggiata diretta, allora sono congiungibili da un cammino diretto. Siano v, $w\in V(G)$ e sia $P=(v_0,v_1,\dots,v_n)$ una passeggiata diretta di lunghezza minima che congiunge v e w e proviamo che P è un cammino diretto. Infatti se per assurdo v_i=v_j con i<j allora $(v_1,\dots v_i,v_{j+1}, \dots , v_n$ sarebbe ancora una passeggiata diretta tra v e w, ma ciò è in contraddizione con il fatto che P sia di lunghezza minima.

La riflessività è ovvia (basta prendere cammini di lunghezza 0, e la transitività, come nel caso dei grafi, si prova congiungendo due passeggiate.

L'essere congiungibili da un cammino diretto non è una relazione d'equivalenza. Basta considerare il seguente esempio: $V=\{0,1\}$ e $E=\{(0,1)\}$. 0 è congiungibile a 1 ma non il viceversa.     

Soluzione dell'esercizio 20.3   $x{\cal R}\circ ({\cal S}\circ {\cal T})w$ se e solo se esiste $y\in Y$ tale che $x{\cal R}y$ e $y {\cal S}\circ {\cal T}w$ e quest'ultima è vera se e solo se esiste $z\in Z$ tale che $y{\cal S}z$ e $z {\cal T}w$. In definitiva

$$x{\cal R}\circ ({\cal S}\circ {\cal T})w \iff \exists y\in Y ... ... R}y \hbox{\rm { e }} y{\cal S}z\hbox{\rm { e }} z {\cal T}w.$$

In modo analogo si ha che $x({\cal R}\circ {\cal S}) \circ {\cal T}$ se e solo se esiste $z\in Z$ tale che $x {\cal R}\circ {\cal S}z$ e $z {\cal T}w$, e la prima equivale a dire che esiste $y\in Y$ tale che $x{\cal R}y$ e $y{\cal S}z$, e quindi:

$$x({\cal R}\circ {\cal S}) \circ {\cal T}w \iff \exists z\in Z... ... R}y \hbox{\rm { e }} y{\cal S}z\hbox{\rm { e }} z {\cal T}w.$$

Evidentemente le due cose coincidono.     

Soluzione dell'esercizio 20.4  

    

Soluzione dell'esercizio 20.5  

    

Soluzione dell'esercizio 20.6  

    

Soluzione dell'esercizio 20.7  

    

Soluzione dell'esercizio 20.8  

    

Soluzione dell'esercizio 20.9  

    

Soluzione dell'esercizio 22.1  

    

Soluzione dell'esercizio 23.1