Lezione 4 (7 marzo 2000 h. 11-13)

Ricordiamo gli assiomi (dovuti a Peano) che descrivono la struttura dei numeri naturali.

Assioma 4.4 (di induzione) se $A\subseteq \mathbb N$ è un sottinsieme tale che

1.: $0\in A$
2.: $\forall n \in \mathbb N\quad (n\in A \Rightarrow\mathop{\rm succ}\nolimits(n) \in A)$

allora $A=\mathbb N$ .

Proposizione 4.5 Sia $n\in\mathbb N$ , $n\ne 0$ allora esiste un unico $m\in\mathbb N$ tale che $\mathop{\rm succ}\nolimits(m) = n$ . Tale m viene chiamato il predecessore di m.

Dimostrazione. Avendo l'esistenza, l'unicità segue immediatamente dall'iniettività di $\mathop{\rm succ}\nolimits$ .

Supponiamo per assurdo che esista un $m\ne 0$ tale che $\mathop{\rm succ}\nolimits(n) \ne m$ per ogni n, allora sia $A = \mathbb N-\{m\}$ . Chiaramente $0\in A$ , in quanto $m\ne 0$ . Se $n \in A$ , allora $succ (n) \ne m$ e quindi $succ (n) \in A$ . Ma allora $A=\mathbb N$ , e questa è una contraddizione. $\square$

A partire dagli assiomi si possono definire ricorsivamente la somma, il prodotto di numeri naturali e il loro ordinamento.

Definizione 4.6 Si definisce la somma di due naturali:

$\begin{displaymath}\begin{array}{rclcl} n+0 & = & n &\quad & \forall n\in\mathb... ...\nolimits(n+m) &\quad & \forall n,m \in \mathbb N \end{array} \end{displaymath}$

Avendo la somma si definisce induttivamente il prodotto:

$\begin{displaymath}\begin{array}{rclcl} n\cdot0 & = & 0 &\quad & \forall n\in\m... ...(n\cdot m) + n &\quad & \forall n,m \in \mathbb N \end{array} \end{displaymath}$

Dalla somma si ricava anche la definizione delll'ordinamento:

$\begin{displaymath}n \le m \iff \exists k \in \mathbb N: n + k = m \end{displaymath}$

Esercizio 4.2 Si provi che $\le$ è un ordinamento totale su $\mathbb N$ e che verifica le seguenti proprietà:

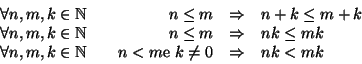
$\begin{displaymath}\begin{array}{rcrcl} \forall n,m,k \in\mathbb N& \quad & n \... ... < m \hbox{\rm {e }} k\ne0 & \Rightarrow& nk < mk \end{array} \end{displaymath}$

Soluzione

Il principio di induzione (prima forma)

Teorema 4.7 (prima forma dell'induzione) Sia P(n) una famiglia di proposizioni indiciate su $\mathbb N$ e si supponga che

1.: P(0) sia vera
2.: per ogni $n\in\mathbb N$ $P(n)\Rightarrow P(n+1)$

allora P(n) è vera per ogni $n\in\mathbb N$

Dimostrazione. Sia $A=\{n\mid P(n)\hbox{\rm { \\lq e vera}}\}$ , allora $0\in A$ e se $n \in A$ anche $n+1\in A$ , quindi per l'assioma di induzione $A=\mathbb N$ . $\square$

L'assioma di buon ordinamento

Definizione 4.8 Un ordinamento totale su un insieme X si dice un buon ordinamento, e in tal caso l'insieme ordinatoo $(X,\le)$ si dice ben ordinato se ogni sottinsieme non vuoto di X ha minimo.

Dimostrazione. Supponiamo che l'insieme $A\subseteq \mathbb N$ non abbia minimo e proviamo che allora $A=\varnothing$ . Chiamiamo B il suo complementare ( $B=\mathbb N-A$ ) e dimostriamo per induzione che

Supponiamo che $\{0,1,\dots,n\}\subseteq B$ , allora $0,1,\dots,n\notin A$ e quindi $n+1 \notin A$ , altrimenti ne sarebbe il minimo, ma allora $n+1 \in B$ e pertanto $\{0,1,\dots,n,n+1\}\subseteq B$ .

Il principio di induzione (seconda forma)

Teorema 4.10 (seconda forma dell'induzione) Sia P(n) una famiglia di proposizioni indiciate su $\mathbb N$ e si supponga che

1.: P(0) sia vera
2.: per ogni n>0 $(P(k) \hbox{\rm { vera }}\forall k<n)\Rightarrow P(n+1)$

allora P(n) è vera per ogni $n\in\mathbb N$

Dimostrazione. Sia $A = \{ n \in\mathbb N\mid P(n)\hbox{\rm { non \\lq e vera}}\}$ , e supponiamo per assurdo che $A\ne\varnothing$ . Allora per la proprietà di buon ordinamento A ha minimo n. Chiaramente $n\ne 0$ in quanto P(0) è vera. Inoltre se k<n allora $k\notin A$ in quanto $n=\min A$ , ma allora dalla (2) segue che P(n) è vera e quindi $n\notin A$ , contraddicendo il fatto che $n \in A$ . $\square$

Osservazione 4.11 Si osservi che sia l'enunciato che la dimostrazione precedenti non usano il fatto che si stia parlando di numeri naturali, ma soltanto che si sta lavorando in un insieme bene ordinato. Quindi il principio di induzione in questa forma è applicabile ad ogni insieme bene ordinato.

La divisione euclidea

Teorema 4.12 Siano $n,m\in\mathbb Z$ con $m\ne 0$ , allora esistono unici $q,r\in \mathbb Z$ tai che

$\begin{displaymath}\begin{array}{l} n = mq + r \\ 0 \le r < \left\vert m\right\vert \end{array} \end{displaymath}$

Dimostrazione. Esistenza. Supponiamo dapprima che $n,m\in\mathbb N$ , ed usiamo il principio di induzione nella seconda forma su n. Se n=0 basta prendere q=0 e r=0. Supponiamo n>0 e che la tesi sia vera per ogni k<n. Se n<m basta prendere q=0 e r=n, altrimenti sia k=n-m, dato che $m\ne 0$ $0 \le k<n$ , quindi per ipotesi di induzione esistono $q,r\in\mathbb N$ tali che

Supponiamo ora n<0 e m>0. Allora -n>0 e quindi per il caso precedente si ha che esistono $q,r\in \mathbb Z$ tali che -n=mq+r e $0\le r<m=\left\vert m\right\vert$ . E quindi n=m(-q)-r. Se r=0 abbiamo finito, se invece 0<r<m allora $0<m-r<m=\left\vert m\right\vert$ e n=m(-q)-r=m(-q)-m+m-r=m(-1-q)+(m-r).

Sia infine m<0 allora -m>0, quindi per i due casi precedenti esistono $q,r\in \mathbb Z$ tali che n=(-m)q+=m(-q)+r con $0\le r<-m=\left\vert m\right\vert$ .

Unicità. Supponiamo che n= mq + r e n=mq'+r' con $0\le r,r'<m$ . Supponiamo che $r'\ge r$ , allora m(q-q')=r'-r e quindi passando ai moduli si ha $\left\vert m\right\vert\left\vert q-q'\right\vert=\left\vert r'-r\right\vert=r'-r<\left\vert m\right\vert$ ,da cui $0\le\left\vert q-q'\right\vert<1$ e quindi $\left\vert q-q'\right\vert=0$ ovvero q=q'. Ma allora da mq+r=mq'+r' segue che anche r=r'. $\square$

Scommettiamo che due di voi hanno lo stesso compleanno?

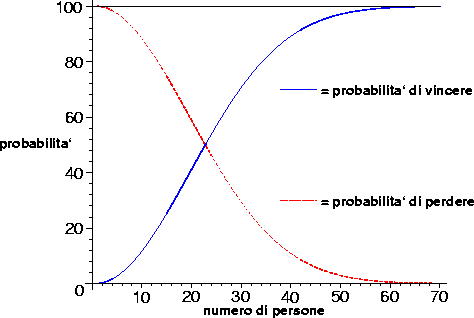
Storiella. Il professore di Matematica Discreta entra nell'aula, davanti ai suoi 60 studenti esclama: --Scommettiamo che due di voi hanno lo stesso compleanno?-- e aggiunge --se io perdo pago la cena a tutti, se vinco voi pagete una cena a me.--

Gli studenti accettano entusiasti la scommessa: --Male che vada ci rimettiamo 1000 lire ciascuno, ma in ogni caso-- pensano --è praticamente impossibile che il prof. vinca, siamo troppo pochi.--

Una rapida verifica e quindi la delusione: il professore, come ogni anno, si è guadagnato una cena.

Perché il prof. ha vinto? È soltanto una fortuna sfacciata, che gli consente di vincere ogni anno, o è qualcos'altro?

Formalizziamo la situazione. Associare ad ogni studente il proprio giorno di nascita è una funzione da un insieme X con 60 elementi (l'insieme degli studenti) in un insieme Y con 365 elementi (l'insieme dei possibili giorni di nascita, escludendo il caso degli anni bisestili). Il professore perde se tale funzione è iniettiva, vince altrimenti. Si tratta allora di contare il numero di funzioni iniettive, e dividerlo per il numero di funzioni, questo darà la probabilità di perdere la scommessa da parte del professore.

Esercizio 4.3 Siano X e Y insiemi finiti di cardinalità rispettivamente k e n, con $k \le n$ . Si provi che l'insieme delle applicazioni iniettive $X\to Y$ ha cardinalità pari a n!/(n-k)!.
Soluzione

Se $\left\vert X\right\vert= k$ e $\left\vert Y\right\vert= n$ la probabilità che una funzione $f:X\to Y$ sia iniettiva è pari a

**Figure 1:** Grafico della probabilità di successo o di insuccesso in funzione del numero di persone. Già con 60 persone si ha la ragionevole certezza di vincere la scommessa: la probabilità di successe è attorno al 99%
$\begin{figure} \begin{center} \leavevmode\psfig{file=complean.ps} \end{center} \end{figure}$