


Next: Lezione 2 (29 febbraio
Up: Matematica Discreta (II modulo)
Previous: Matematica Discreta (II modulo)
Subsections
Insiemi e operazioni tra insiemi
Non intendiamo qui dare un'assiomatica della teoria degli insiemi, per noi un
insieme sarà soltanto una collezione di oggetti detti i suoi elementi.
La proprietà fondamentale che si richied affinché un oggetto sia un insieme
è che si possa sempre stabilire senza ambiguità se qualche cosa è un suo
elemento oppure no. In simboli, se A è un insieme allora per ogni x si ha
che 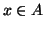 (x appartiene ad A) oppure
(x appartiene ad A) oppure 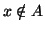 (x non
appartiene ad A). Questa che può sembrare una richiesta vuota in realtà
non lo è. Si consideri l'oggetto definito da:
(x non
appartiene ad A). Questa che può sembrare una richiesta vuota in realtà
non lo è. Si consideri l'oggetto definito da:
e si provi a stabilire se 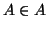 oppure no.
oppure no.
- 1.
- Se
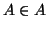 ,
allora, dalla definizione di A segue che
,
allora, dalla definizione di A segue che
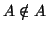
- 2.
- Se
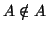 allora, per definizione di A,
allora, per definizione di A, 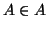
Quindi A non può essere un insieme, in quanto non possiamo decidere se 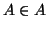 oppure no. Questo esempio è noto come il paradosso di Russel.
oppure no. Questo esempio è noto come il paradosso di Russel.
L'altra proprietà fondamentale degli insiemi, e che fornisce un criterio per
stabilire quando due insiemi sono uguali, è la seguente
Assioma 1.1 (estensionalità)
Due insiemi sono uguali se e solo se hanno gli stessi elementi. In simboli
Ricordiamo alcune definizioni.
Definizione 1.2
Siano
X e
Y due insiemi, si dice che
X è
contenuto in
Y (o
anche
X è
sottinsieme di
Y), e si denota con
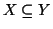
se
ogni elemento di
X è elemento di
Y, in simboli,
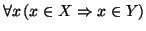
.
Si dice che
X è
contenuto strettamente in
Y (o anche che è un
sottinsieme proprio di
Y) e si denota con
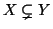
,
se
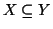
e
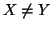
.
Se X e Y sono insiemi si costruiscono altri insiemi:
Se
I è un insieme e per ogni
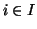
è dato un insieme
Xi, si
definiscono
- intersezione
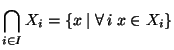
- unione
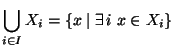
Esercizio 1.2
Siano
X e
Y insiemi, si provi che
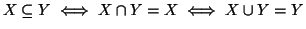
.
Soluzione
Esercizio 1.3
Siano
X,
Y,
Z insiemi, si provino le seguenti:
- 1.
- proprietà associativa dell'intersezione e dell'unione
- 2.
- proprietà commutativa
- 3.
- proprietà di assorbimento
- 4.
- proprietà distributiva dell'intersezione rispetto all'unione e
dell'unione rispetto all'intersezione
- 5.
- leggi di de Morgan
- 6.
-
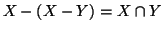
- 7.
- se
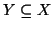 allora
allora
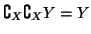 .
.
Soluzione
Esercizio 1.4
Siano
X,
Y,
Z insiemi, si provino le seguenti:
- 1.
-
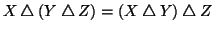
- 2.
-
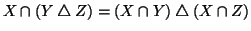
Soluzione
Equipotenza di insiemi
Definizione 1.3
Siano
X e
Y due insiemi, diremo che
X e
Y sono
equipotenti se
esiste una bigezione
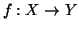
.
Denoteremo questo fatto con
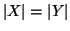
,
che leggeremo anche
X e
Y hanno la stessa cardinalità.
Osservazione 1.4
Si osservi che non stiamo dando alcun significato al simbolo
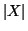
,
ossia
non stiamo definendo cosa sia la
cardinalità di un insieme. In effetti
ciò può essere fatto (e sarà fatto in corsi successivi), ossia si
possono definire una classe di particolari insiemi detti
cardinali che
godono della seguente proprietà:
ogni insieme è equipotente ad uno ed un solo cardinale.
Quando questo sarà fatto, quello che per noi è una definizione, ossia
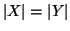
se e solo se esiste una bigezione tra
X e
Y, sarà un
teorema.
Proposizione 1.5
Valgono le seguenti proprietà:
- 1.
- X è equipotente a se stesso.
- 2.
- se X è equipotente a Y allora X è equipotente a X
- 3.
- se X è equipotente a Y e Y è equipotente a Z, allora X è
equipotente a Z.
Dimostrazione.
L'identità è una bigezione; se f è una bigezione, allora f-1 è
una bigezione; composizione di bigezioni è una bigezione.

Esercizio 1.5
Siano
X,
Y,
X',
Y' insiemi e siano
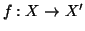
e
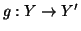
due
applicazioni. Si definisca
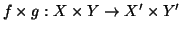
ponendo
Si provi che
- 1.
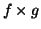 è surgettiva se e solo se f e g sono entrambe
surgettive.
è surgettiva se e solo se f e g sono entrambe
surgettive.
- 2.
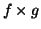 è iniettiva se e solo se f e g sono entrambe
iniettive.
è iniettiva se e solo se f e g sono entrambe
iniettive.
Soluzione
Esercizio 1.8
Si provi che se
X,
Y,
Z sono insiemi, allora
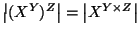
.
Soluzione
Esercizio 1.9
Si provi che se
X,
Y,
Z sono insiemi con
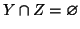
,
allora
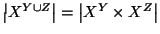
.
Soluzione
Insiemi finiti: il Lemma dei cassetti
Dato un numero naturale
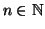 denotiamo con In l'insieme
denotiamo con In l'insieme
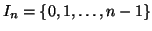 .
.
Definizione 1.6
Diremo che un insieme è
finito se esiste
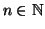
tale che
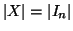
.
Un insieme è detto
infinito se non è finito
Teorema 1.7 (Lemma dei cassetti)
Siano
X e
Y due insiemi aventi rispettivamente
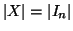
e
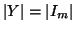
con
n<
m allora ogni applicazione
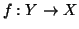
non è
iniettiva.
Dimostrazione.
Procediamo per induzione su n. Se n=0 allora
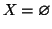 e
e
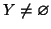 ,
quindi l'insieme XY delle applicazioni
,
quindi l'insieme XY delle applicazioni 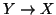 è vuoto, e quindi non c'è
nulla da dimostrare (dal falso segue ogni cosa).
è vuoto, e quindi non c'è
nulla da dimostrare (dal falso segue ogni cosa).
Supponiamo che la tesi sia vera per n e proviamola per n+1. Sia
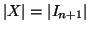 e sia,
e sia,
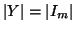 con m>n+1 e supponiamo per
assurdo che l'applicazione
con m>n+1 e supponiamo per
assurdo che l'applicazione 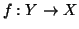 sia iniettiva. Per definizione esiste una
bigezione
sia iniettiva. Per definizione esiste una
bigezione
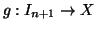 ;
poniamo xn=g(n) e
;
poniamo xn=g(n) e
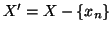 .
Chiaramente
X' è in bigezione con In. Si hanno due casi:
.
Chiaramente
X' è in bigezione con In. Si hanno due casi:
- 1.
-
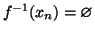 (i.e.
(i.e.
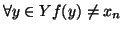 )
)
- 2.
-
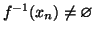 (i.e.
(i.e.
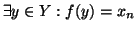 )
)
Nel primo caso,
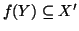 e quindi
e quindi 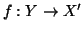 sarebbe un'applicazione
iniettiva da un insieme equipotente a Im in un insieme equipotente a In;
dato che m>n+1>n questo è assurdo per ipotesi di induzione.
sarebbe un'applicazione
iniettiva da un insieme equipotente a Im in un insieme equipotente a In;
dato che m>n+1>n questo è assurdo per ipotesi di induzione.
Nel secondo caso, sia  tale che f(y)=xn e sia
tale che f(y)=xn e sia
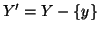 .
Dato che
f è iniettiva,
.
Dato che
f è iniettiva,
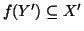 e quindi,
e quindi,
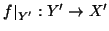 è una applicazione iniettiva. Dato che
è una applicazione iniettiva. Dato che
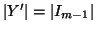 ,
,
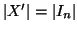 e m-1>n, ciò è assurdo per ipotesi di induzione.
e m-1>n, ciò è assurdo per ipotesi di induzione.

Corollario 1.8
Se
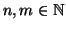
sono due naturali diversi
X e
Y sono insiemi finiti con
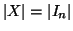
e
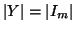
,
allora
X e
Y non sono
equipotenti.
In particolare, se
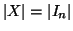
e
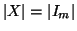
allora
n=
m.
Si osservi che questo corollario fa sì che si possa definire la
cardinalità degli insiemi finiti.
Definizione 1.9
Sia
X un insieme finito, si dice
cardinalità di
X l'unico numero
naturale
n tale che
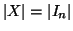
.
Osservazione 1.10
Il nome lemma dei cassetti deriva dal seguente modo naif di enunciare il
teorema precedente: se ho un certo numero di oggetti da sistemare in dei
cassetti, e il numero di oggetti è superiore a quello dei cassetti, almeno
un cassetto conterrà più di un oggetto.
Proposizione 1.11
Sia
X un insieme finito e
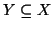
allora anche
Y è finito e
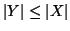
.
Se
Y è un sottoinsieme proprio di
X allora
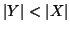
.
Dimostrazione. Procediamo per induzione su
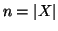 .
Se n=0 allora
.
Se n=0 allora
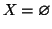 e
quindi anche
e
quindi anche
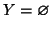 ,
da cui si conclude. Supponiamo la tesi vera per n e
sia dato X con
,
da cui si conclude. Supponiamo la tesi vera per n e
sia dato X con
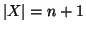 .
Sia
.
Sia
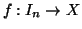 una bigezione e sia, poniamo
xn=f(n) e
una bigezione e sia, poniamo
xn=f(n) e
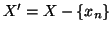 .
Chiaramente
.
Chiaramente
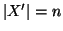 .
Si hanno due casi
.
Si hanno due casi
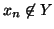 e
e 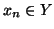 .
Nel primo caso
.
Nel primo caso
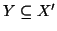 ,
quindi, per ipotesi
di induzione,
,
quindi, per ipotesi
di induzione,
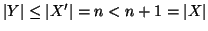 .
Nel secondo caso, detto
.
Nel secondo caso, detto
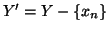 si ha che
si ha che
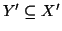 e quindi
e quindi
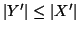 e
quindi
e
quindi
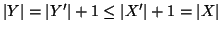 .
Si osservi che in
quest'ultimo caso, se
.
Si osservi che in
quest'ultimo caso, se 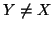 allora anche
allora anche 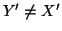 e quindi, per ipotesi di
induzione si ha che
e quindi, per ipotesi di
induzione si ha che
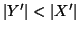 da cui
da cui
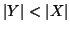 .
.

Come conseguenza si ha il seguente
Corollario 1.12
Un insieme finito non è equipotente ad alcun suo sottoinsieme proprio.
Esempio 1.13
L'insieme
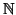
non è finito, si consideri ad esempio
l'applicazione
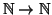
definita da
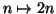
,
questa è una bigezione tra
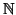
ed il sottinsieme proprio dei numeri pari.
Esercizio 1.10
Siano
X e
Y insiemi finiti. Si provi che
- 1.
- se
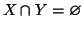 allora
allora
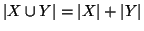 .
.
- 2.
- in generale
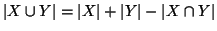
Soluzione
Esercizio 1.11
Siano
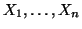
insiemi finiti a due a due disgiunti si provi che
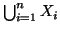
è finito e che
Soluzione
Esercizio 1.12
Se
X e
Y sono insiemi finiti, si provi che
- 1.
-
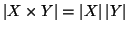 .
.
- 2.
-
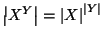
- 3.
-
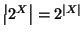 .
.
Soluzione
Esercizio 1.13
Siano
X e
Y insiemi finiti entrambi di cardinalità
n. Si provi che
ogni funzione iniettiva
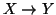
è anche surgettiva.
Soluzione
Esercizio 1.14
Sia
X un insieme finito di cardinalità
n. Si determini il numero delle
applicazioni biunivoche di
X in sé.
Soluzione



Next: Lezione 2 (29 febbraio
Up: Matematica Discreta (II modulo)
Previous: Matematica Discreta (II modulo)
Domenico Luminati
2000-06-14
![]() la differenza X-Y viene chiamata il complemento di Y in X e viene denotata anche con
la differenza X-Y viene chiamata il complemento di Y in X e viene denotata anche con
![]() o semplicemente con
o semplicemente con
![]() o con Y' quando non ci sia ambiguità
o con Y' quando non ci sia ambiguità
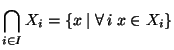
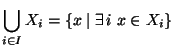
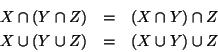
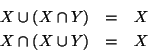
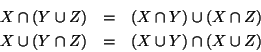
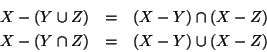
![]()
![]() e
e
![]() ,
quindi l'insieme XY delle applicazioni
,
quindi l'insieme XY delle applicazioni ![]() è vuoto, e quindi non c'è
nulla da dimostrare (dal falso segue ogni cosa).
è vuoto, e quindi non c'è
nulla da dimostrare (dal falso segue ogni cosa).
![]() e sia,
e sia,
![]() con m>n+1 e supponiamo per
assurdo che l'applicazione
con m>n+1 e supponiamo per
assurdo che l'applicazione ![]() sia iniettiva. Per definizione esiste una
bigezione
sia iniettiva. Per definizione esiste una
bigezione
![]() ;
poniamo xn=g(n) e
;
poniamo xn=g(n) e
![]() .
Chiaramente
X' è in bigezione con In. Si hanno due casi:
.
Chiaramente
X' è in bigezione con In. Si hanno due casi:
![]() tale che f(y)=xn e sia
tale che f(y)=xn e sia
![]() .
Dato che
f è iniettiva,
.
Dato che
f è iniettiva,
![]() e quindi,
e quindi,
![]() è una applicazione iniettiva. Dato che
è una applicazione iniettiva. Dato che
![]() ,
,
![]() e m-1>n, ciò è assurdo per ipotesi di induzione.
e m-1>n, ciò è assurdo per ipotesi di induzione.
![]()
![]() .
Se n=0 allora
.
Se n=0 allora
![]() e
quindi anche
e
quindi anche
![]() ,
da cui si conclude. Supponiamo la tesi vera per n e
sia dato X con
,
da cui si conclude. Supponiamo la tesi vera per n e
sia dato X con
![]() .
Sia
.
Sia
![]() una bigezione e sia, poniamo
xn=f(n) e
una bigezione e sia, poniamo
xn=f(n) e
![]() .
Chiaramente
.
Chiaramente
![]() .
Si hanno due casi
.
Si hanno due casi
![]() e
e ![]() .
Nel primo caso
.
Nel primo caso
![]() ,
quindi, per ipotesi
di induzione,
,
quindi, per ipotesi
di induzione,
![]() .
Nel secondo caso, detto
.
Nel secondo caso, detto
![]() si ha che
si ha che
![]() e quindi
e quindi
![]() e
quindi
e
quindi
![]() .
Si osservi che in
quest'ultimo caso, se
.
Si osservi che in
quest'ultimo caso, se ![]() allora anche
allora anche ![]() e quindi, per ipotesi di
induzione si ha che
e quindi, per ipotesi di
induzione si ha che
![]() da cui
da cui
![]() .
.
![]()