


Next: Lezione 3 (6 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 1 (28 febbraio
Subsections
Insiemi infiniti: l'assioma della scelta
Uno degli strumenti più potenti di cui si ha spesso bisogno quando si deve
trattare con insiemi infiniti, è il seguente:
Assioma 2.1 (della scelta)
Sia
I un insieme e per ogni
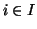
sia dato un insieme
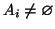
.
Allora esiste una funzione, detta
funzione di scelta,
tale che
Osservazione 2.2
Questo assioma dice essenzialmente che quando si ha un insieme di insiemi non
vuotiè possibile scegliere, in un colpo solo, un elemento da ciascuno
di essi. Si osservi che questo assioma è non costruttivo per
antonomasia: ci dice che una funzione di scelta esiste, ma non dà alcun modo
per trovarla.
Esercizio 2.1
Si provi che una funzione
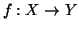
è surgettiva se e solo se esiste
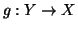
tale che
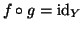
.
Una tale
g si chiama una
inversa
destra di
f.
Soluzione
Esercizio 2.2
Si provi che una funzione
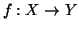
è iniettiva se e solo se esiste
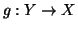
tale che
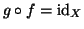
.
Una tale
g si chiama una
inversa
sinistra di
f.
Soluzione
Teorema 2.3
Se
X è un insieme infinito, allora contiene un sottinsieme
Y con
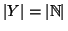
.
Dimostrazione.
Sia
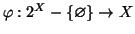 una funzione di scelta e, dato un elemento
una funzione di scelta e, dato un elemento
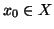 consideriamo la funzione
consideriamo la funzione
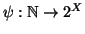 definita
ricorsivamente da:
definita
ricorsivamente da:
e quindi definiamo la funzione
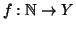 ponendo f(0)=x0 e per ogni
n>0,
ponendo f(0)=x0 e per ogni
n>0,
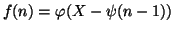 .
Osserviamo che, dalla definizione di
.
Osserviamo che, dalla definizione di 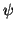 segue che per ogni
segue che per ogni
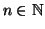 si ha
si ha
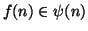 e
e
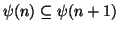 ,
da cui segue che se
,
da cui segue che se 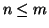 allora
allora
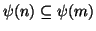 e
quindi
e
quindi
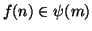 .
Ma allora se n < m,
.
Ma allora se n < m,
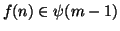 ,
mentre
,
mentre
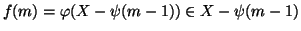 e quindi
e quindi
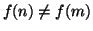 ,
pertanto fè iniettiva. L'insieme
,
pertanto fè iniettiva. L'insieme
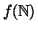 è allora l'insieme cercato.
è allora l'insieme cercato.

Osservazione 2.4
In qualche senso il teorema precedente mostra come la cardinalità dei numeri
naturali sia,
in un senso ancora da specificare la ``più piccola'' tra le
cardinalità infinite.
Proposizione 2.5
Ogni insieme infinito è equipotente ad un suo sottinsieme proprio.
Dimostrazione. Sia X un insieme infinito e sia
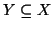 un sottinsieme
equipotente a
un sottinsieme
equipotente a 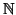 .
Abbiamo già visto che
.
Abbiamo già visto che 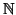 è equipotente ad un suo sottinsieme
proprio, quindi se
è equipotente ad un suo sottinsieme
proprio, quindi se
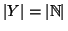 ,
Y è equipotente ad un suo
sottinsieme proprio, in parrtcolare esiste una bigezione
,
Y è equipotente ad un suo
sottinsieme proprio, in parrtcolare esiste una bigezione 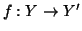 essendo
essendo
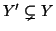 .
Ma allora la funzione
.
Ma allora la funzione 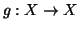 definita da
definita da
dà una bigezione tra X ed il sottinsieme
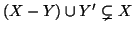 .
.

La proposizione precedente ed il corollario 1.12, provano la
seguente caratterizzazione degli insiemi infiniti.
Teorema 2.6
Un insieme è infinito se e solo se è equipotente ad un suo sottinsieme
proprio.
Insiemi numerabili
Definizione 2.7
Un insieme
X si dice
numerabile se
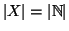
.
La
cardinalità di
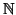
viene spesso indicata con
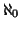
(si legge aleph
con zero). Quindi per dire che
X è numerabile si scriverà anche
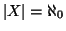
.
Il simbolo 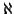 la prima lettera dell'alfabeto ebraico.
la prima lettera dell'alfabeto ebraico.
Diamo ora alcune proprietà degli insiemi numerabili.
Proposizione 2.8
Se
X e
Y sono insiemi numerabili disgiunti, allora
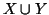
è
numerabile.
Dimostrazione. Siano
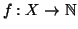 e
e
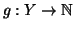 due bigezioni, allora si definisca
due bigezioni, allora si definisca
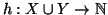 ponendo
ponendo
Si verifica facilmente che h è una bigezione.

Proposizione 2.9
Se
X e
Y sono disgiunti,
X numerabile e
Y è finito, allora
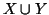
è numerabile.
Siano
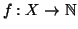 e
e
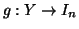 due bigezioni, allora si definisca
due bigezioni, allora si definisca
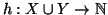 ponendo
ponendo
Si verifica facilmente che h è una bigezione.

Dimostrazione.
Se Y non è finito, allora contiene un sottinsieme numerabile Z, ma allora
la tesi segue dal lemma 3.4.

Proposizione 2.11
Se
X è un insieme infinito ed
Y è un insieme finito o numerabile
allora
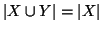
.
Dimostrazione. Possiamo supporre che Y sia disgiunto da X, in quanto
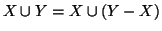 e per la proposizione precedente e la proposizione 1.11
Y-X è finito o numerabile.
e per la proposizione precedente e la proposizione 1.11
Y-X è finito o numerabile.
Sia
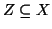 un sottinsieme numerabile, per le due proposizioni 2.9,
2.8, esiste una bigezione
un sottinsieme numerabile, per le due proposizioni 2.9,
2.8, esiste una bigezione
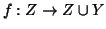 .
Si definisca
allora
.
Si definisca
allora
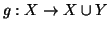 ponendo
ponendo
Proviamo che g è iniettiva. Siano
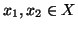 diversi, chiaramente,
dato che f è iniettiva, se
diversi, chiaramente,
dato che f è iniettiva, se
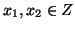 allora
allora
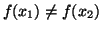 e quindi
e quindi
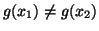 .
Se
.
Se
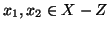 ,
evidentemente
,
evidentemente
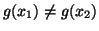 .
Se
.
Se
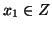 e
e
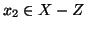 allora
allora
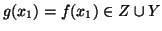 e, dato che Y è
disgiunto da X,
e, dato che Y è
disgiunto da X,
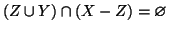 ,
e quindi
,
e quindi
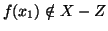 ,
mentre
,
mentre
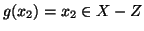 .
.
Proviamo che g è surgettiva. Sia
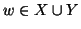 ,
allora si hanno due casi:
,
allora si hanno due casi:
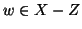 oppure
oppure
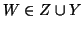 .
Nel primo caso, preso x=w, si ha che
g(x)=w. Nel secondo caso, dato che f è surgettiva, esiste
.
Nel primo caso, preso x=w, si ha che
g(x)=w. Nel secondo caso, dato che f è surgettiva, esiste 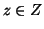 tale
che f(z)=w, e quindi g(z)=w.
tale
che f(z)=w, e quindi g(z)=w.

Proposizione 2.12
Se
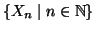
è una famiglia numerabile di insiemi finiti e a
due a due disgiunti, allora
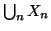
è numerabile.
Dimostrazione. Sia
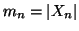 e per ogni n sia
e per ogni n sia
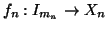 una
bigezione. Si considerino i numeri
una
bigezione. Si considerino i numeri
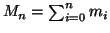 ,
M-1=0, e si
definisca
,
M-1=0, e si
definisca
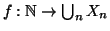 ponendo
ponendo
Una semplice verifica mostra che f è ben definita ed è una bigezione.

Proposizione 2.13
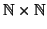
è numerabile, e quindi il prodotto di due insiemi numerabili
è numerabile.
Dimostrazione.
Per ogni
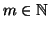 si consideri
si consideri
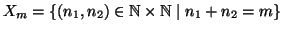 .
Chiaramente
.
Chiaramente
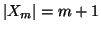 per ogni m,
per ogni m,
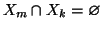 se
se
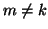 e infine
e infine
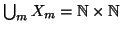 (si osservi che
(si osservi che
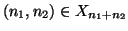 ). Ma allora la tesi segue dalla proposizione
precedente.
). Ma allora la tesi segue dalla proposizione
precedente.
Per quanto riguarda la seconda parte dell'enunciato, si osservi che se X e Y
sono numerabili, e
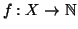 e
e
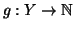 sono bigezioni, allora
l'applicazione prodotto
sono bigezioni, allora
l'applicazione prodotto
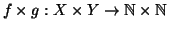 è
bigettiva.
è
bigettiva.

Proposizione 2.14
Se
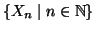
è una famiglia numerabile di insiemi numerabili e
a due a due disgiunti, allora
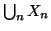
è numerabile.
Dimostrazione.
Per ogni
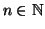 sia
sia
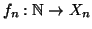 una bigezione, definiamo
una bigezione, definiamo
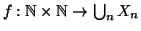 ponendo
f(n,m)=fn(m). Si conclude
verificando che f è una bigezione.
ponendo
f(n,m)=fn(m). Si conclude
verificando che f è una bigezione.

Esercizio 2.3
Si eseguano nel dettaglio tutte le verifiche necessarie a concludere le
dimostrazioni delle proposizioni di questa sezione.
Soluzione
Esercizio 2.4
Si provi che se
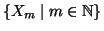
è una famiglia numerabile di insiemi
finiti, allora la loro unione è finita o numerabile.
Soluzione
Esercizio 2.5
Si provi che se
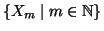
è una famiglia numerabile di insiemi
numerabili, allora la loro unione è numerabile.
Soluzione
Esercizio 2.6
Si provi che
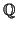
è numerabile.
Soluzione



Next: Lezione 3 (6 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 1 (28 febbraio
Domenico Luminati
2000-06-14
![]() una funzione di scelta e, dato un elemento
una funzione di scelta e, dato un elemento
![]() consideriamo la funzione
consideriamo la funzione
![]() definita
ricorsivamente da:
definita
ricorsivamente da:
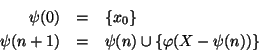
![]() un sottinsieme
equipotente a
un sottinsieme
equipotente a ![]() .
Abbiamo già visto che
.
Abbiamo già visto che ![]() è equipotente ad un suo sottinsieme
proprio, quindi se
è equipotente ad un suo sottinsieme
proprio, quindi se
![]() ,
Y è equipotente ad un suo
sottinsieme proprio, in parrtcolare esiste una bigezione
,
Y è equipotente ad un suo
sottinsieme proprio, in parrtcolare esiste una bigezione ![]() essendo
essendo
![]() .
Ma allora la funzione
.
Ma allora la funzione ![]() definita da
definita da
![]() e
e
![]() due bigezioni, allora si definisca
due bigezioni, allora si definisca
![]() ponendo
ponendo
![]()
![]() e per la proposizione precedente e la proposizione 1.11
Y-X è finito o numerabile.
e per la proposizione precedente e la proposizione 1.11
Y-X è finito o numerabile.
![]() un sottinsieme numerabile, per le due proposizioni 2.9,
2.8, esiste una bigezione
un sottinsieme numerabile, per le due proposizioni 2.9,
2.8, esiste una bigezione
![]() .
Si definisca
allora
.
Si definisca
allora
![]() ponendo
ponendo
![]() ,
allora si hanno due casi:
,
allora si hanno due casi:
![]() oppure
oppure
![]() .
Nel primo caso, preso x=w, si ha che
g(x)=w. Nel secondo caso, dato che f è surgettiva, esiste
.
Nel primo caso, preso x=w, si ha che
g(x)=w. Nel secondo caso, dato che f è surgettiva, esiste ![]() tale
che f(z)=w, e quindi g(z)=w.
tale
che f(z)=w, e quindi g(z)=w.
![]()
![]() e per ogni n sia
e per ogni n sia
![]() una
bigezione. Si considerino i numeri
una
bigezione. Si considerino i numeri
![]() ,
M-1=0, e si
definisca
,
M-1=0, e si
definisca
![]() ponendo
ponendo
![]() si consideri
si consideri
![]() .
Chiaramente
.
Chiaramente
![]() per ogni m,
per ogni m,
![]() se
se
![]() e infine
e infine
![]() (si osservi che
(si osservi che
![]() ). Ma allora la tesi segue dalla proposizione
precedente.
). Ma allora la tesi segue dalla proposizione
precedente.
![]() e
e
![]() sono bigezioni, allora
l'applicazione prodotto
sono bigezioni, allora
l'applicazione prodotto
![]() è
bigettiva.
è
bigettiva.
![]()
![]() sia
sia
![]() una bigezione, definiamo
una bigezione, definiamo
![]() ponendo
f(n,m)=fn(m). Si conclude
verificando che f è una bigezione.
ponendo
f(n,m)=fn(m). Si conclude
verificando che f è una bigezione.
![]()