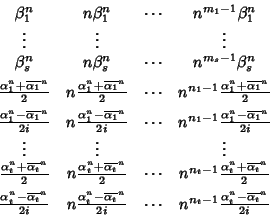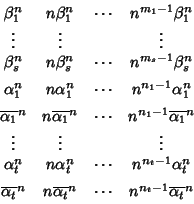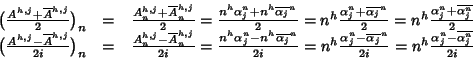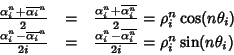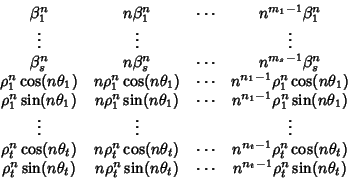Next: Lezione 22 (3 maggio
Up: Matematica Discreta
Previous: Lezione 20 (28 aprile
Subsections
Definizione 21.1
Si dice che un campo
K è
algebricamente chiuso se ogni polinomio non
nullo di
K[
x] ha almeno una radice. In simboli
Vale il seguente teorema di cui omettiamo la dimostrazione.
Teorema 21.2 (Fondamentale dell'algebra)
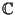
è algebricamente chiuso
Teorema 21.3
Sia
K un campo algebricamente chiuso e sia
![$P\in K[x]$](img738.gif)
con
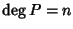
.
Allora esistono
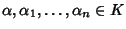
tali che
Dim.
Procediamo per induzione su 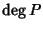 .
Se
.
Se 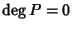 non c'è niente da
dimostrare. Sia
non c'è niente da
dimostrare. Sia
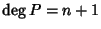 con
con 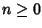 ,
allora, dato che K è
algebricamente chiuso e P non è costante, esiste
,
allora, dato che K è
algebricamente chiuso e P non è costante, esiste
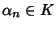 tale che
tale che
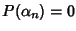 .
Per il teorema di Ruffini si ha allora che
.
Per il teorema di Ruffini si ha allora che
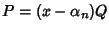 e
e
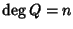 .
Ma allora per
ipotesi di induzione
.
Ma allora per
ipotesi di induzione
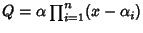 e quindi
e quindi
Ciò conclude la dimostrazione.

Osservazione 21.4
Osserviamo che gli
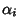
che compaiono nella fattorizzazione del
teorema precedente sono esattamente le radici di
P, e se in
tale fattorizzazione si raccolgono tra loro i fattori uguali, si ottiene una
fattorizzazione del tipo
essendo
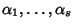
le radici distinte di
P e
mi le
rispettive
molteplicità. Si ha pertanto il seguente
Corollario 21.5
Sia
K algebricamente chiuso e
![$P\in K[x]$](img738.gif)
.
Se
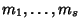
sono
le molteplicità delle radici di
P, allora
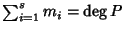
.
Osservazione 21.6
Grazie a questo corollario ed al fatto che
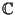 è
algebricamente chiuso
è
algebricamente chiuso si ha allora che le successioni nella tesi del teorema
20.8 sono esattamente
k.
Proposizione 21.7
Sia
![$P\in\mathbb R[x]$](img886.gif)
e sia
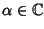
una radice di
P di molteplicità
m. Allora anche
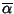
è una radice di
P di molteplicità
m.
Dim.
Ricordiamo che la coniugazione
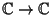 è un morfismo di anelli e che se
è un morfismo di anelli e che se
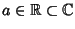 allora
allora
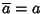 .
.
Sia
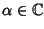 una radice di
una radice di
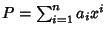 con
con
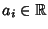 .
Allora:
.
Allora:
Quindi
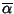 è una radice di P.
è una radice di P.
Sia m la molteplicità di 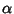 allora
allora
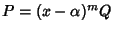 con
con
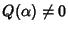 .
Sia ora n la molteplicità della radice
.
Sia ora n la molteplicità della radice
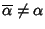 .
Il fatto che
.
Il fatto che
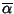 è una radice di P di
molteplicità n e
è una radice di P di
molteplicità n e
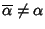 garantisce e che
garantisce e che
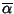 è
una radice di Q con la stessa molteplicità. Ossia
è
una radice di Q con la stessa molteplicità. Ossia
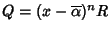 con
con
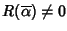 ,
ossia
,
ossia
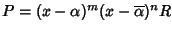 con
con
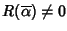 e
e
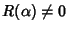 .
Supponiamo che
.
Supponiamo che 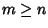 (ciò non
è restrittivo a meno di scambiare i ruoli di
(ciò non
è restrittivo a meno di scambiare i ruoli di 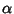 e
e
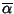 ),
allora
),
allora
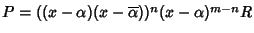 .
Osserviamo che
.
Osserviamo che
e quindi, per il l'unicità della divisione euclidea anche
![$S=
(x-\alpha)^{m-n}R\in\mathbb R[x]$](img903.gif) .
Se per assurdo m>n allora
.
Se per assurdo m>n allora 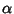 sarebbe una
radice di S e quindi anche
sarebbe una
radice di S e quindi anche
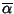 sarebbe radice di S, ma
sarebbe radice di S, ma
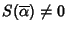 dato che
dato che
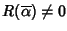 e
e
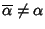 .
.

Supponiamo di avere ora una equazione ricorsiva reale e sia
![$P\in\mathbb R[x]$](img886.gif) il
suo polinomio caratteristico. P avrà alcune radici reali
il
suo polinomio caratteristico. P avrà alcune radici reali
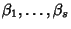 di molteplicità
di molteplicità
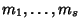 ,
ed alcune radici
non reali, che, per quanto visto sopra, sono accoppiate dal
coniugio. Siano
,
ed alcune radici
non reali, che, per quanto visto sopra, sono accoppiate dal
coniugio. Siano
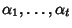 e
e
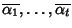 le radici non reali e
le radici non reali e
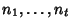 le loro molteplicità (ni è la molteplicità di
le loro molteplicità (ni è la molteplicità di 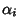 e di
e di
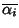 ).
).
Teorema 21.8
Le successioni
sono una base reale dello spazio vettoriale
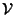
delle soluzioni
dell'equazione ricorsiva reale.
Dim.
Per il teorema 20.8 si ha che le successioni
sono una base dello spazio delle soluzioni complesse dell'equazione
ricorsiva. Per ogni h e j indichiamo con Ah,j la successione
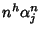 e con
e con
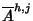 la successione
la successione
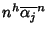 .
Osserviamo che lo spazio generato da Ah,j e
.
Osserviamo che lo spazio generato da Ah,j e
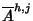 è lo stesso di quello generato da
è lo stesso di quello generato da
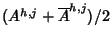 e
e
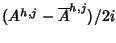 ,
quindi nella base complessa dello
spazio
,
quindi nella base complessa dello
spazio 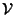 si possono sostituire le successioni Ah,j e
si possono sostituire le successioni Ah,j e
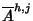 con le successioni
con le successioni
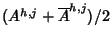 e
e
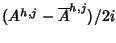 ottenendo ancora una base di
ottenendo ancora una base di
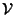 .
Ma ora
.
Ma ora
sono successioni reali. Da ciò segue allora la tesi.

Osservazione 21.9
Si osservi che se
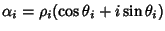
,
allora
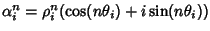
e quindi
Ma allora la base dello spazio
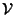
data nel
teorema
precedente può essere riscritta come:



Next: Lezione 22 (3 maggio
Up: Matematica Discreta
Previous: Lezione 20 (28 aprile
Domenico Luminati
1999-07-08
![]() .
Se
.
Se ![]() non c'è niente da
dimostrare. Sia
non c'è niente da
dimostrare. Sia
![]() con
con ![]() ,
allora, dato che K è
algebricamente chiuso e P non è costante, esiste
,
allora, dato che K è
algebricamente chiuso e P non è costante, esiste
![]() tale che
tale che
![]() .
Per il teorema di Ruffini si ha allora che
.
Per il teorema di Ruffini si ha allora che
![]() e
e
![]() .
Ma allora per
ipotesi di induzione
.
Ma allora per
ipotesi di induzione
![]() e quindi
e quindi
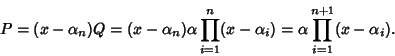
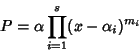
![]() è un morfismo di anelli e che se
è un morfismo di anelli e che se
![]() allora
allora
![]() .
.
![]() una radice di
una radice di
![]() con
con
![]() .
Allora:
.
Allora:
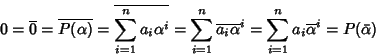
![]() allora
allora
![]() con
con
![]() .
Sia ora n la molteplicità della radice
.
Sia ora n la molteplicità della radice
![]() .
Il fatto che
.
Il fatto che
![]() è una radice di P di
molteplicità n e
è una radice di P di
molteplicità n e
![]() garantisce e che
garantisce e che
![]() è
una radice di Q con la stessa molteplicità. Ossia
è
una radice di Q con la stessa molteplicità. Ossia
![]() con
con
![]() ,
ossia
,
ossia
![]() con
con
![]() e
e
![]() .
Supponiamo che
.
Supponiamo che ![]() (ciò non
è restrittivo a meno di scambiare i ruoli di
(ciò non
è restrittivo a meno di scambiare i ruoli di ![]() e
e
![]() ),
allora
),
allora
![]() .
Osserviamo che
.
Osserviamo che
![]() il
suo polinomio caratteristico. P avrà alcune radici reali
il
suo polinomio caratteristico. P avrà alcune radici reali
![]() di molteplicità
di molteplicità
![]() ,
ed alcune radici
non reali, che, per quanto visto sopra, sono accoppiate dal
coniugio. Siano
,
ed alcune radici
non reali, che, per quanto visto sopra, sono accoppiate dal
coniugio. Siano
![]() e
e
![]() le radici non reali e
le radici non reali e
![]() le loro molteplicità (ni è la molteplicità di
le loro molteplicità (ni è la molteplicità di ![]() e di
e di
![]() ).
).