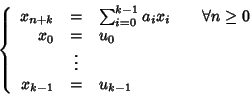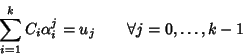Next: Lezione 21 (29 aprile
Up: Matematica Discreta
Previous: Lezione 19 (26 aprile
Subsections
Dim.
Si consideri l'applicazione
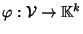 definita da
definita da
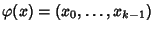 .
Dimostreremo che
.
Dimostreremo che 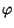 è lineare e iniettiva
da cui seguirà allora la tesi.
è lineare e iniettiva
da cui seguirà allora la tesi.
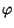 è lineare. Infatti se x,y sono successioni e
è lineare. Infatti se x,y sono successioni e
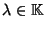 ,
allora
,
allora
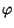 è iniettiva. Per fare ciò proviamo che
è iniettiva. Per fare ciò proviamo che
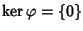 .
Sia
.
Sia
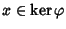 ,
proviamo per induzione su n che allora xn=0 per ogni
n. Se
,
proviamo per induzione su n che allora xn=0 per ogni
n. Se 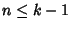 xn=0 dato che
xn=0 dato che
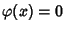 .
Supponiamo
.
Supponiamo 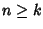 e
supponiamo che la tesi sia vera per ogni h< n. Allora
e
supponiamo che la tesi sia vera per ogni h< n. Allora
dave si è usato il fatto che n-k+i < n per ogni
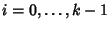 e quindi
l'ipotesi di induzione.
e quindi
l'ipotesi di induzione.

Osservazione 20.3
Osserviamo che 0 non può essere radice del polinomio caratteristico di
una equazione ricorsiva, infatti
P(0)=
a0 e quindi 0 è radice se e
solo se
a0=0. Ma se fosse
a0=0 allora vorrebbe dire che l'equazione
ricorsiva
avrebbe ordine k-1.
Proposizione 20.4
La successione
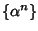
è soluzione dell'equazione (
27) se
solo se
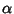
è radice del polinomio caratteristico.
Dim.
La successione
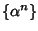 è soluzione dell'equazione
ricorsiva se e solo se
si ha
è soluzione dell'equazione
ricorsiva se e solo se
si ha
ossia se e solo se
Dato che la successione
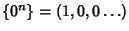 non è soluzione
dell'equazione ricorsiva (per questa successione xk=0 mentre
non è soluzione
dell'equazione ricorsiva (per questa successione xk=0 mentre
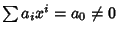 ),e per quanto osservato sopra 0 non è radice del polinomio
caratteristico, possiamo dividere per
),e per quanto osservato sopra 0 non è radice del polinomio
caratteristico, possiamo dividere per 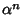 l'equazione
precedente ottenendo che
l'equazione
precedente ottenendo che
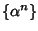 è soluzione se e solo se
è soluzione se e solo se
che è la tesi.

Lemma 20.5
Siano
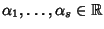
numeri a due a due distinti, allora le
successioni
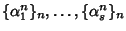
sono linearmente
indipendenti.
Dim.
Siano
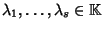 tali che la successione
tali che la successione
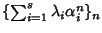 sia la successione nulla, ovvero
sia la successione nulla, ovvero
in particolare allora
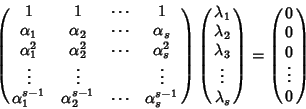
Tale relazione può essere riscritta in termini matriciali come:
ma la matrice di tale sistema è invertibile e quindi
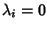 per ogni
per ogni
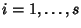 .
.

Teorema 20.6
Supponiamo che il polinomio caratteristico dell'equazione (
27) abbia
k radici distinte
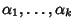
allora le successioni
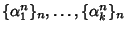
sono una base di
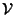
.
Dim.
Per la proposizione 20.4 le successioni
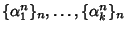 sono soluzioni dell'equazione
ricorsiva; per il lemma precedente
sono linearmente indipendenti. Dato che
sono soluzioni dell'equazione
ricorsiva; per il lemma precedente
sono linearmente indipendenti. Dato che
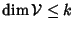 , costituiscono una base di
, costituiscono una base di 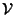 .
.

Osservazione 20.7
Si osservi che come immediata conseguenza del teorema precedente si ha che
la dimensione di
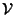
è proprio
k e quindi l'applicazione
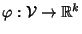
definita nella dimostrazione della proposizione
20.1 è un isomorfismo. Pertanto, dati
k numeri
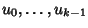
,
il problema di Cauchy di trovare una successione tale
che
ha una e una sola soluzione. Si ha anche un metodo per determinarne una
soluzione esplicita: una generica soluzione è data da
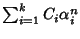
con
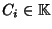
.
Basterà quindi determinare le costanti
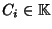
in modo da verificare le condizioni inizialoi e precisamente in modo che
e questo è un sistema lineare, che si sa risolvere.
Nel caso generale vale il seguente teorema di cui omettiamo la dimostrazione.
Teorema 20.8
Sia
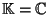
e siano
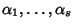
le radici del polinomio
caratteristico dell'equazione ricorsiva. Siano
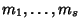
le rispettive
molteplicità. Allora le
successioni
sono una base dello spazio vettoriale
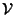
.
Osservazione 20.9
Si vedrà nella prossima lezione che il numero di tali successioni è, anche
in questo caso, esattamente
k, e quindi tutto quanto detto
nell'
osservazione precedente resta vero anche nelle ipotesi di questo teorema.



Next: Lezione 21 (29 aprile
Up: Matematica Discreta
Previous: Lezione 19 (26 aprile
Domenico Luminati
1999-07-08
![]() definita da
definita da
![]() .
Dimostreremo che
.
Dimostreremo che ![]() è lineare e iniettiva
da cui seguirà allora la tesi.
è lineare e iniettiva
da cui seguirà allora la tesi.
![]() è lineare. Infatti se x,y sono successioni e
è lineare. Infatti se x,y sono successioni e
![]() ,
allora
,
allora
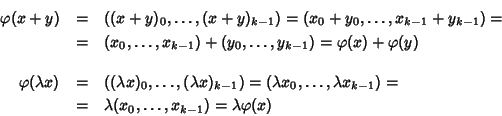
![]() è iniettiva. Per fare ciò proviamo che
è iniettiva. Per fare ciò proviamo che
![]() .
Sia
.
Sia
![]() ,
proviamo per induzione su n che allora xn=0 per ogni
n. Se
,
proviamo per induzione su n che allora xn=0 per ogni
n. Se ![]() xn=0 dato che
xn=0 dato che
![]() .
Supponiamo
.
Supponiamo ![]() e
supponiamo che la tesi sia vera per ogni h< n. Allora
e
supponiamo che la tesi sia vera per ogni h< n. Allora
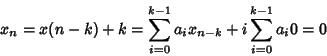
![]() è soluzione dell'equazione
ricorsiva se e solo se
si ha
è soluzione dell'equazione
ricorsiva se e solo se
si ha
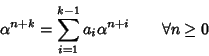
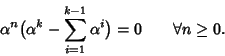
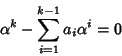
![]() tali che la successione
tali che la successione
![]() sia la successione nulla, ovvero
sia la successione nulla, ovvero
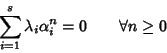
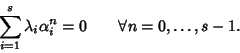
![]() sono soluzioni dell'equazione
ricorsiva; per il lemma precedente
sono linearmente indipendenti. Dato che
sono soluzioni dell'equazione
ricorsiva; per il lemma precedente
sono linearmente indipendenti. Dato che
![]() , costituiscono una base di
, costituiscono una base di ![]() .
.
![]()