Dim.
1G=1G1G e quindi
![]() .
Moltiplicando a sinistra per
l'inverso di
.
Moltiplicando a sinistra per
l'inverso di
![]() segue che
segue che
![]() .
.
1G=gg-1 e quindi
![]() .
Moltiplicando entrambi i
membri a sinistra per
.
Moltiplicando entrambi i
membri a sinistra per
![]() si ottiene
si ottiene
![]() .
.
![]()
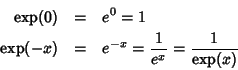
Dim.
Siano
![]() ,
e chiamiamo
,
e chiamiamo
![]() e
e
![]() .
Dato che
.
Dato che ![]() è un morfismo
è un morfismo
Dim.
La 1 della proposizione 13.1, garantisce che
![]() ,
e quindi
,
e quindi
![]() .
.
Siano
![]() ,
allora, usando la 2 di proposizione
13.1 ed il fatto che
,
allora, usando la 2 di proposizione
13.1 ed il fatto che
![]() ,
,
Sia ora
![]() e
e ![]() ,
allora
,
allora
![]() ,
e quindi, per la proposizione
12.1,
,
e quindi, per la proposizione
12.1,
![]() è normale.
è normale.
![]()
Dim.
Se ![]() è iniettivo, allora necessariamente
è iniettivo, allora necessariamente
![]() ha un solo
elemento (si troverebbero altrimenti due elementi distinti aventi per immagine
1) e poiché
ha un solo
elemento (si troverebbero altrimenti due elementi distinti aventi per immagine
1) e poiché
![]() si ha che
si ha che
![]() .
.
Viceversa siano
![]() tali che
tali che
![]() ,
allora
,
allora
Dim.
Per quanto osservato precedentemente, l'esistenza di una unica applicazione che faccia commutare il
diagramma, e che tale applicazione verifichi le condizioni 1 e 2, è garantita dal teorema di omomorfismo per
insiemi. Per avere
la tesi, dobbiamo soltanto mostrare che tale applicazione è un morfismo,
ossia che
![]() .
Ma,
usando la commutatività del diagramma, ed
il fatto osservato precedentemente, che
.
Ma,
usando la commutatività del diagramma, ed
il fatto osservato precedentemente, che ![]() è un morfismo, si ha:
è un morfismo, si ha:
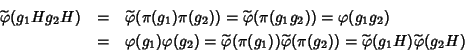
Dim.
Sia g un generatore di G, e si consideri l'applicazione
![]() definita da
definita da
![]() .
Il fatto che
g(h+k)=ghgk, per ogni
.
Il fatto che
g(h+k)=ghgk, per ogni
![]() mostra che
mostra che ![]() è un morfismo. D'altra parte, dato che g è
un generatore di G,
è un morfismo. D'altra parte, dato che g è
un generatore di G, ![]() è
surgettivo, ma allora per quanto osservato sopra, G è isomorfo a
è
surgettivo, ma allora per quanto osservato sopra, G è isomorfo a
![]() .
D'altra parte i
sottogruppi di
.
D'altra parte i
sottogruppi di ![]() sono tutti e soli della forma
sono tutti e soli della forma
![]() con
con ![]() ,
quindi
G è isomorfo o a
,
quindi
G è isomorfo o a
![]() ,
e ciò si ha solo se Gè infinito, oppure
,
e ciò si ha solo se Gè infinito, oppure
![]() ed in tal caso o(G)=n.
ed in tal caso o(G)=n.
![]()