Lezione 12 (2 aprile 2001 h. 9.30-10.30)

Il teorema cinese del resto

Teorema 12.1 (Cinese del resto)   Il sistema di congruenze

$$\left\{ \begin{array}{rcl} x&\cong &a\quad{\rm mod} n \\ x&\cong &b\quad{\rm mod} m \end{array} \right.$$

ha soluzione se e solo se $(n,m)\mathrel{\big\vert}b-a$.

Se $c$ è una soluzione del sistema, allora gli elementi di $\left[c\right]_{[n,m]}$ sono tutte e sole le soluzioni del sistema (i.e. le soluzioni sono tutte e sole della forma $c+k[n,m]$ al variare di $k\in\mathbb{Z}$).

Dimostrazione.  Sia $c$ una soluzione del sistema allora esistono $h,k\in\mathbb{Z}$ tali che $c=a+hn=b+km$ e quindi $a-b=km-hn$. Ma allora dal fatto che $(n,m)\mathrel{\big\vert}n$ e $(n,m)\mathrel{\big\vert}m$ si ha che $(n,m)\mathrel{\big\vert}a-b$. Viceversa, supponiamo che $(n,m)\mathrel{\big\vert}a-b$, allora esistono $h,k\in\mathbb{Z}$ tali che $a-b=hn+km$. Ma allora $a-hn=b+kn$, detto quindi $c=a-hn=b+kn$, si ha evidentemente che $c$ risolve entrambe le congruenze.

Sia $S=\{x\in\mathbb{Z}\mid x \hbox{\rm { risolve il sistema}}\}$. Dobbiamo provare che se $c$ è una soluzione allora $S=\left[c\right]_{[n,m]}$.

$S\subseteq\left[c\right]_{[n,m]}$. Sia $c'$ un'altra soluzione, allora $c=a+hn=b+km$ e $c'=a+h'n=b+k'm$ e quindi sottraendo si ha

$$\begin{array}{rclcl} c-c'&=&a+hn-a'-h'n=(h-h')n &\Rightarr... ...m=(k-k')m &\Rightarrow &m\mathrel{\big\vert}(c-c') \end{array}$$

Ma allora $[n,m]\mathrel{\big\vert}c-c'$ ossia $c'\cong c\quad{\rm mod} [n,m]$ ovvero $c'\in\left[c\right]_{[n,m]}$.

$\left[c\right]_{[n,m]}\subseteq S$. Sia $c'\in\left[c\right]_{[n,m]}$, ovvero $c'=c+h[n,m]$. Dal fatto che $c\cong a \quad{\rm mod} n$ e che $h[n,m]\cong 0\quad{\rm mod} n$ segue che $c'=c+h[n,m]\cong a \quad{\rm mod} n$. In modo analogo si ha che $c'\cong b\quad{\rm mod} m$ e quindi che $c'\in S$.     $\square$

Esercizio 12.1   Siano $n_1,\dots,n_k$ interi a due a due primi tra loro. Si provi che il sistema di congruenze

$$\left\{\begin{array}{rcll} x & \cong & a_1 & \quad{\rm mod... ...\ x & \cong & a_k & \quad{\rm mod} n_k \end{array}\right.$$

ammette soluzione e che se $c$ è una soluzione, tutte le altre sono del tipo $c + k n_1\cdot\dots\cdot n_k]$.
Soluzione

Esercizio 12.2   Siano $\varepsilon _0,\varepsilon _1,\dots,\varepsilon _k$ le cifre della espressione decimale del numero $n$. Si provi che

1. $3\mathrel{\big\vert}n \iff 3\mathrel{\big\vert}(\varepsilon _0+\varepsilon _1+\dots+\varepsilon _k)$
2. $9\mathrel{\big\vert}n \iff 9\mathrel{\big\vert}(\varepsilon _0+\varepsilon _1+\dots+\varepsilon _k)$
3. $11\mathrel{\big\vert}n \iff 11\mathrel{\big\vert}(\varepsilon _0-\varepsilon _1+\dots+(-1)^k\varepsilon _k)$

Soluzione

Elementi invertibili modulo $n$

Definizione 12.2   Sia $a \in \mathbb{Z}$ diremo che $a$ è invertibile modulo $n$ se esiste $x\in\mathbb{Z}$ tale che $a x \cong 1\quad{\rm mod} n$ (in $\mathbb{Z}\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb{Z}}} {{}_{\!\texts... ... {{}_{\!\scriptstyle {}n\mathbb{Z}}} {{}_{\!\scriptscriptstyle {}n\mathbb{Z}}}$). Un tale $x$ si dice un inverso di $a$ modulo $n$.

Proposizione 12.3   $a$ è invertibile modulo $n$ se e solo se $(a,n)=1$.

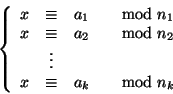
Dimostrazione.  Se $a$ è invertibile e $x$ è un suo inverso, allora $n\mathrel{\big\vert}(ax-1)$, quindi esiste $k$ tale che $nk=ax-1$ e quindi $1=nk-ax$, da cui $1=(a,n)$.

Viceversa, se $1=(a,n)$ allora esistono $\alpha,\beta\in\mathbb{Z}$ tali che $1=a\alpha+n\beta$, ma allora $a\alpha\cong 1\quad{\rm mod} n$.     $\square$

Proposizione 12.4   Siano $x,y$ due inversi di $a$ modulo $n$, allora $x=y$ (in $\mathbb{Z}\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb{Z}}} {{}_{\!\texts... ... {{}_{\!\scriptstyle {}n\mathbb{Z}}} {{}_{\!\scriptscriptstyle {}n\mathbb{Z}}}$).

Dimostrazione. Dal fatto che $ax=1$ in $\mathbb{Z}\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb{Z}}} {{}_{\!\texts... ... {{}_{\!\scriptstyle {}n\mathbb{Z}}} {{}_{\!\scriptscriptstyle {}n\mathbb{Z}}}$, moltiplicando entrambi i membri per $y$, ed usando le proprietà associativa, commutativa e dell'$1$ si ottiene

$$\left[y\right]_n= \left[1\right]_n\left[y\right]_n = (\left[... ...right]_n)= \left[x\right]_n\left[1\right]_n = \left[x\right]_n$$

    $\square$

Proposizione 12.5   Sia $a$ invertibile modulo $n$ e sia $a'= a$ in $\mathbb{Z}\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb{Z}}} {{}_{\!\texts... ... {{}_{\!\scriptstyle {}n\mathbb{Z}}} {{}_{\!\scriptscriptstyle {}n\mathbb{Z}}}$ allora anche $a'$ è invertibile e $a$ e $a'$ hanno gli stessi inversi.

Dimostrazione.  Se $ax=i$ in $\mathbb{Z}\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb{Z}}} {{}_{\!\texts... ... {{}_{\!\scriptstyle {}n\mathbb{Z}}} {{}_{\!\scriptscriptstyle {}n\mathbb{Z}}}$ allora $n\mathrel{\big\vert}(ax-1)$, se $a'= a$ in $\mathbb{Z}\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb{Z}}} {{}_{\!\texts... ... {{}_{\!\scriptstyle {}n\mathbb{Z}}} {{}_{\!\scriptscriptstyle {}n\mathbb{Z}}}$ allora esiste $k$ tale che $a'=a+kn$. Ma allora $a'x-1=ax-1+knx$ è divisibile per $n$ e quindi $a'x=1$ in $\mathbb{Z}\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb{Z}}} {{}_{\!\texts... ... {{}_{\!\scriptstyle {}n\mathbb{Z}}} {{}_{\!\scriptscriptstyle {}n\mathbb{Z}}}$.     $\square$

Osservazione 12.6   Osserviamo che le due proposizioni precedenti permettono di definire l'invertibilità e l'inverso di una classe di congruenza. Diremo che $\left[a\right]_n$ è invertibile se e solo se $a$ è invertibile modulo $n$ (la seconda delle proposizioni assicura che tale definizione dipende solo dalla classe e non dal rappresentante) e permette di d. Se $\left[a\right]$ è invertibile, l'insieme degli inversi di $a$ (che dipende solo dalla classe e non dal rappresentante) formano una classe di congruenza, che viene chiamata l'inverso di $\left[a\right]_n$ e denotata con $\left[a\right]_n^{-1}$.

La proposizione 12.3 può allora essere rienunciata

Proposizione 12.7   $\left[a\right]_n$ è invertibile se e solo se $(a,n)=1$.

Corollario 12.8   Se $p$ è primo, ogni elemento non nullo di $\mathbb{Z}\big/\mathchoice {{}_{\!\displaystyle {}p\mathbb{Z}}} {{}_{\!\texts... ... {{}_{\!\scriptstyle {}p\mathbb{Z}}} {{}_{\!\scriptscriptstyle {}p\mathbb{Z}}}$ è invertibile.

Dimostrazione.  Se $a\ne0$ in $\mathbb{Z}\big/\mathchoice {{}_{\!\displaystyle {}p\mathbb{Z}}} {{}_{\!\texts... ... {{}_{\!\scriptstyle {}p\mathbb{Z}}} {{}_{\!\scriptscriptstyle {}p\mathbb{Z}}}$ allora $p\not\mathrel{\big\vert}a$ e quindi, dato che $p$ è primo, $(p,a)=1$, da cui la tesi.     $\square$