

Next: Lezione 10 (28 marzo
Up: Matematica Discreta
Previous: Lezione 8 (21 marzo
Subsections
Definizione 9.1
Dati due interi
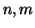
si dice che

è un
divisore di
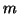
(o che
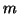
è un
multiplo di

) se esiste un
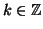
tale
che
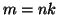
. Si indica con
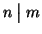
(si legge
 divide
divide
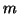
).
Esempio 9.2
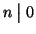
per ogni

mentre se
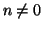
allora
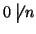
, si ha
inoltre che
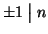
e
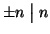
per ogni

.
Dimostrazione.
1. Se 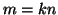 e
e 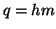 allora
allora 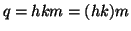 ossia
ossia
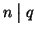 .
.
2. Se 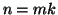 e
e 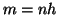 allora
allora 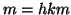 e quindi
e quindi
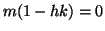 e quindi o
e quindi o 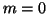 e quindi anche
e quindi anche 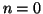 , oppure
, oppure 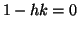 ma
allora o
ma
allora o 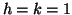 e quindi
e quindi 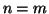 oppure
oppure 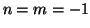 e quindi
e quindi 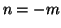 .
.

Definizione 9.4
Il numero

si dice
primo se i suoi unici divisori sono
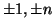
.
Proposizione 9.6
Se
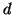
e
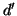
sono due massimi comun divisori tra

e
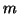
allora
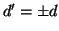
.
Dimostrazione.
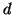 è un divisore comune di
è un divisore comune di  e
e 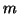 , quindi poiché
, quindi poiché 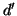 è un massimo comun divisore si ha che
è un massimo comun divisore si ha che
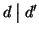 . Scambiando i
ruoli di
. Scambiando i
ruoli di 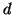 e
e 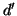 si ha allora che anche
si ha allora che anche
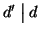 e quindi per
9.3 si ha che
e quindi per
9.3 si ha che 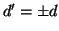 .
.

Definizione 9.7
Diremo che
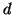
è
il massimo comun divisore di

e
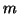
se
è un massimo comun divisore positivo. La proposizione precedente
garantisce che se esiste il massimo comun divisore è unico. Esso
verrà indicato con
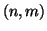
.
Teorema 9.8
Dati due numeri
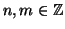
non entrambi nulli esiste il massimo
comun divisore di

ed
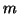
.
Dimostrazione.
Si consideri l'insieme
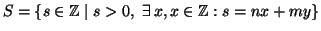 .
.
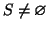 dato che
dato che 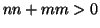 (dato che
(dato che  e
e 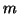 non sono entrambi nulli). Sia
non sono entrambi nulli). Sia
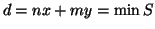 , dimostriamo che
, dimostriamo che 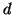 è il massimo comun divisore. Se
è il massimo comun divisore. Se
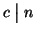 e
e
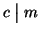 allora
allora
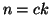 e
e 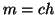 , quindi
, quindi
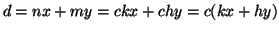 ossia
ossia
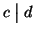 . Dimostriamo ora che
. Dimostriamo ora che
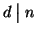 . Consideriamo la divisione
euclidea tra
. Consideriamo la divisione
euclidea tra  e
e 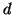 ossia
ossia 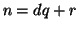 con
con 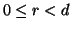 , se
, se  allora
allora
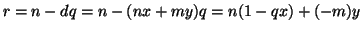 è un elemento di
è un elemento di 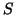 . Ciò è
assurdo perché
. Ciò è
assurdo perché 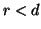 e
e 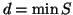 . Quindi
. Quindi 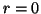 ossia
ossia
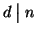 .
In modo analogo si prova che
.
In modo analogo si prova che
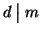 .
.

Osservazione 9.9
Dalla dimostrazione precedente segue che dati
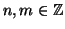
esistono
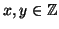
tali che
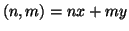
e che gli interi della forma
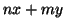
con
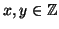
sono tutti e soli i multipli di
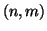
.
Definizione 9.10
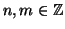
non entrambi nulli si dicono
coprimi se
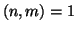
.
Dimostrazione.
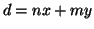 e quindi
e quindi
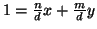 .
.

Proposizione 9.13 (algoritmo di Euclide)
Siano
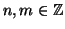
,
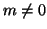
. Sia
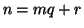
la divisione euclidea di

per
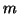
allora
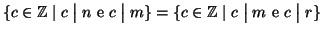
, in
particolare quindi
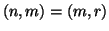
.
Dimostrazione.
Se
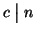 e
e
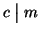 allora
allora 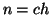 e
e 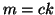 e quindi
e quindi
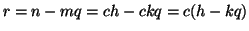 ossia
ossia
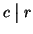 e
e
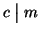 . Viveversa
se
. Viveversa
se
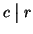 e
e
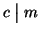 allora
allora 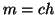 e
e 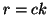 e quindi
e quindi
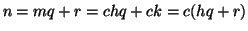 ossia
ossia
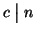 e
e
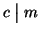 .
.

Osservazione 9.14
La proposizione precedente assieme all'osservazione che
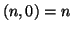
per
ogni
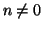
permette di costruire un algoritmo (
algoritmo di
Euclide) per il calcolo del M.C.D.
tale algoritmo si può tradurre in un programma ricorsivo per la definizione di
una funzione
MCD che calcoli il M.C.D. tra due numeri naturali:

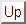

Next: Lezione 10 (28 marzo
Up: Matematica Discreta
Previous: Lezione 8 (21 marzo
Luminati Domenico
2002-06-07
![]() e
e ![]() allora
allora ![]() ossia
ossia
![]() .
.
![]() e
e ![]() allora
allora ![]() e quindi
e quindi
![]() e quindi o
e quindi o ![]() e quindi anche
e quindi anche ![]() , oppure
, oppure ![]() ma
allora o
ma
allora o ![]() e quindi
e quindi ![]() oppure
oppure ![]() e quindi
e quindi ![]() .
.
![]()
![]() è un divisore comune di
è un divisore comune di ![]() e
e ![]() , quindi poiché
, quindi poiché ![]() è un massimo comun divisore si ha che
è un massimo comun divisore si ha che
![]() . Scambiando i
ruoli di
. Scambiando i
ruoli di ![]() e
e ![]() si ha allora che anche
si ha allora che anche
![]() e quindi per
9.3 si ha che
e quindi per
9.3 si ha che ![]() .
.
![]()
![]() .
.
![]() dato che
dato che ![]() (dato che
(dato che ![]() e
e ![]() non sono entrambi nulli). Sia
non sono entrambi nulli). Sia
![]() , dimostriamo che
, dimostriamo che ![]() è il massimo comun divisore. Se
è il massimo comun divisore. Se
![]() e
e
![]() allora
allora
![]() e
e ![]() , quindi
, quindi
![]() ossia
ossia
![]() . Dimostriamo ora che
. Dimostriamo ora che
![]() . Consideriamo la divisione
euclidea tra
. Consideriamo la divisione
euclidea tra ![]() e
e ![]() ossia
ossia ![]() con
con ![]() , se
, se ![]() allora
allora
![]() è un elemento di
è un elemento di ![]() . Ciò è
assurdo perché
. Ciò è
assurdo perché ![]() e
e ![]() . Quindi
. Quindi ![]() ossia
ossia
![]() .
In modo analogo si prova che
.
In modo analogo si prova che
![]() .
.
![]()
![]() e quindi
e quindi
![]() .
.
![]()
![]() e
e
![]() allora
allora ![]() e
e ![]() e quindi
e quindi
![]() ossia
ossia
![]() e
e
![]() . Viveversa
se
. Viveversa
se
![]() e
e
![]() allora
allora ![]() e
e ![]() e quindi
e quindi
![]() ossia
ossia
![]() e
e
![]() .
.
![]()

