Lezione 23 (5 maggio 1999 h. 9.30-10.30)

Dim. Per definizione di $\varepsilon$ , dati $r\in R$ e $m\in \mathop{\rm Max}\nolimits R$ , si ha che $M\in\varepsilon(r)$ se e solo se $r\notin M$ . Ma allora le due relazioni date dal lemma precedente possono essere riscritte

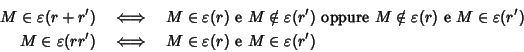
$\begin{eqnarray*}M \in \varepsilon(r+r') & \iff & M\in\varepsilon(r) \hbox{\rm {... ...& \iff & M\in\varepsilon(r) \hbox{\rm { e }} M\in\varepsilon(r') \end{eqnarray*}$

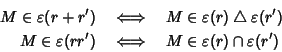
$\begin{eqnarray*}M \in \varepsilon(r+r') & \iff & M\in\varepsilon(r)\bigtriangle... ... \varepsilon(rr') & \iff & M\in\varepsilon(r)\cap\varepsilon(r') \end{eqnarray*}$

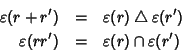
$\begin{eqnarray*}\varepsilon(r+r') & = &\varepsilon(r)\bigtriangleup\varepsilon(r') \\ \varepsilon(rr') & = & \varepsilon(r)\cap\varepsilon(r') \end{eqnarray*}$

Proviamo ora che $\varepsilon$ porta l'identità di R nell'identità di ${\cal P}(\mathop{\rm Max}\nolimits R)$ , ossia che $\varepsilon(1)=\mathop{\rm Max}\nolimits R$ . Infatti se $M\in \mathop{\rm Max}\nolimits R$ allora $M\ne R$ quindi $1\notin R$ , ossia $M\in \varepsilon(1)$ .

$\varepsilon$ è iniettivo. Supponiamo che $\varepsilon(r)=\varnothing$ , allora, dato che $\varepsilon$ è un morfismo di anelli con identità, $\varepsilon(1+r)=\varepsilon(1)\bigtriangleup\varepsilon(r)=\max R\bigtriangleup\varnothing=\mathop{\rm Max}\nolimits R$ . Allora 1+r è invertibile, altrimenti esisterebbe un ideale massimale che lo contiene. Ma allora per l'esercizio 22.3 1+r=1 e quindi r=0.

Proviamo l'ultima parte dell teorema. Dato che R è finito, anche $\mathop{\rm Max}\nolimits R$ lo è e quindi anche tutti i suoi sottoinsiemi lo sono. Sia allora $X\subseteq\mathop{\rm Max}\nolimits R$ e proviamo per induzione sul numero di elementi di X che allora esiste $r\in R$ tale che $\varepsilon(r)=X$ . Se X ha 0 elementi, allora $X=\varnothing$ e $\varepsilon(0)=\varnothing$ . Supponiamo che X abbia un solo elemento, ossia $X=\{M\}$ . Dato che R è finito $R\setminus M$ è finito (e non vuoto perché $M\ne R$ ), sia $R\setminus M=\{x_1,\dots,x_s\}$ . Consideriamo $r=x_1\dots x_s$ il prodotto di tali x_i. Usando il lemma 22.8, si ha

$\begin{displaymath}\begin{array}[b]{rcrcrcrcr} x_1\notin M \\ & \vcenter to 0... ... x_1\cdots x_s\notin M \\ & & & & & & x_s\notin M \end{array}\end{displaymath}$

quindi $M\in\varepsilon(r)$ . D'altra parte se $N\in\mathop{\rm Max}\nolimits R$ e $N\ne M$ allora $N\not\subseteq M$ (altrimenti non sarebbe massimale) e quindi esiste i tale che $x_i\in N$ . Dato che N è un ideale, $r=x_1\cdots x_i \cdots x_s\in N$ e quindi $N\notin \varepsilon(r)$ . Pertanto $\varepsilon(r)=\{M\}=X$ .

Supponiamo ora che X abbia n+1 elementi, allora possiamo scrivere $X= Y\cup Z$ con $Z\cap Y=\varnothing$ e Z costituito da un solo elemento. Allora Yha n elementi, per ipotesi di induzione esiste r tale che $\varepsilon(r)=Y$ e per il caso n=1 esiste r' tale che $\varepsilon(r')=Z$ . Ma allora

$\begin{displaymath}\varepsilon(r+r') = \varepsilon(r) \bigtriangleup\varepsilon(... ...(Y \cup Z) \setminus (Y \cap Z) = X \setminus \varnothing= X. \end{displaymath}$

Definizione di insieme parzialmente ordinato

Definizione 23.1 Sia X un insieme, una relazione $\le$ su X si dirà un ordinamento parziale se

1.: è riflessiva: $x \le x$ per ogni $x\in X$ ;
2.: è antisimmetrica: $x\le y$ e $y\le x \Rightarrow x=y$ ;
3.: è transitiva: $x,le y, y\le z\Rightarrow x\le z$ .

Un ordinamento parziale si dirà un ordinamento totale se in più

1.: per ogni $x,y\in X$ si ha che o $x\le y$ o $y\le x$ .

Una coppia $(X,\le)$ , dove $\le$ è un ordinamento parziale, si dirà un insieme parzialmente ordinato, se $\le$ è un ordinamento totale sidirà un insieme totalmente ordinato o anche una catena.

Esempio 23.2 Gli insiemi $\mathbb N$ , $\mathbb Z$ , $\mathbb Q$ , $\mathbb R$ dotati dell'ordinamento naturale, sono degli insiemi totalmente ordinati.

Sia X un insieme, allora la relazione di inclusione $\subseteq$ è un ordinamento sull'insieme delle sue parti ${\cal P}(X)$ .

La relazione $\big\vert$ è un ordinamento parziale sull'insieme $\mathbb N$ dei numeri naturali.

Esercizio 23.1 Se $Y\subset X$ e $\le$ è un ordinamento su X, la relazione su Y $\le_Y=\le\cap Y\times Y$ è ancora un ordinamento che viene chiamato l'ordinamento indotto da $\le$ su Y.
Soluzione

Esercizio 23.2 Se $\le$ è un ordinamento parziale su X allora la relazione $\ge$ definita da $x \ge y \iff y \le x$ è un ordinamento su X, che viene chiamato l'ordinamento inverso
Soluzione

Definizione 23.3 Sia X un insieme parzialmente ordinato e sia $a\in X$ e $Y\subseteq X$ si dirà che:

a è massimo di X se:	$x\le a$ per ogni $x\in X$
a è minimo di X se:	$a\le x$ per ogni $x\in X$
a è maggiorante di Y se:	$y\le a$ per ogni $y\in Y$
a è minorante di Y se:	$a\le y$ per ogni $y\in Y$
a è estremo superiore di Y se:	a è minimo dei maggioranti di Y
	(i.e. $y\le x$ per ogni $y\in Y\Rightarrow a\le y$ )
a è estremo inferiore di Y se:	a è massimo dei minoranti di Y
	(i.e. $x\le y$ per ogni $y\in Y\Rightarrow y\le a$ )
a è massimale:	$a \le x \Rightarrow x=a$
a è minimale:	$x \le a \Rightarrow x=a$

Esercizio 23.3 Si provi che in $(\mathbb N,\big\vert)$ gli insiemi del tipo $\{a,b\}$ hanno sempre estremo inferiore ed estremo superiore.
Soluzione

Esercizio 23.4 Sia X un insieme parzialmente ordinato, $Y\subset X$ . Si provino le seguenti asserzioni:

1.: Il minimo di X se esiste è unico.
2.: il massimo di X se esiste è unico.
3.: L'estremo inferiore di Y se esiste è unico.
4.: L'estremo superiore di Y se esiste è unico.
5.: Se a è minimo di X allora a è minimale. È vero il viceversa?
6.: Se a è massimo di X allora a è massimale. È vero il viceversa?
7.: se a è minimo di Y allora a è anche estremo inferiore. È vero il viceversa?
8.: se a è massimo di Y allora a è anche estremo superiore. È vero il viceversa?

Soluzione

Ordinamento degli anelli booleani

Prima dimostrazione. La relazione è riflessiva. Infatti se $a\in R$ allora, poicé R è booleano, a=aa e quindi $a\le a$ .

La relazione è antisimmetrica. Se $a\le b$ e $b\le c$ allora, per definizione di $\le$ , a=ab e b=ba. Dato che R è commutativo, ab=ba e quindi a=b.

La relazione è transitiva. Se $a\le b$ e $b\le c$ allora a=ab e b=bc. Sostituiendo la seconda nella prima si ha allora che a=abced usando di nuovo la prima abc=ac e quindi a=ac, ossia $a\le c$ .

Seconda dimostrazione. Sia $\varepsilon$ il morfismo del teorema di rappresentazione. Allora, dato che $\varepsilon$ è iniettivo, si ha:

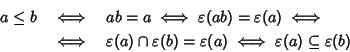
$\begin{eqnarray*}a\le b & \iff & ab=a \iff \varepsilon(ab)=\varepsilon(a) \iff \... ...silon(b)=\varepsilon(a)\iff\varepsilon(a)\subseteq\varepsilon(b) \end{eqnarray*}$

Nel seguito, quando parleremo di ordinamento di un anello booleano, ci riferiremo sempre a quello definito dalla precedente proprsizione.

Lezione 23 (5 maggio 1999 h. 9.30-10.30)

Dimostrazione del teorema di rappresentazione

Definizione di insieme parzialmente ordinato

Ordinamento degli anelli booleani