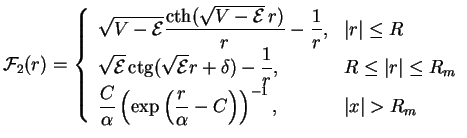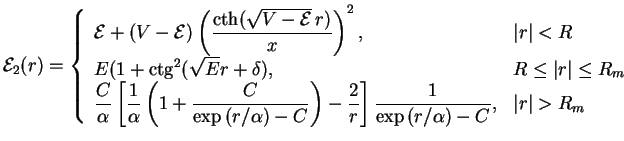Next: Trial wave function of
Up: Three-dimensional wave functions
Previous: Hard sphere trial wave
Contents
Soft sphere trial wave function
At short distances the scattering solution 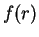 (1.55) is expected
to proved a good approximation for the two-body Bijl-Jastrow term
(1.55) is expected
to proved a good approximation for the two-body Bijl-Jastrow term 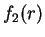 (2.37) in a gas with the soft sphere interaction potential (1.52). At
the larger distances
(2.37) in a gas with the soft sphere interaction potential (1.52). At
the larger distances 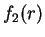 should saturate to a constant in a smooth way. We
choose an exponential type of decay:
should saturate to a constant in a smooth way. We
choose an exponential type of decay:
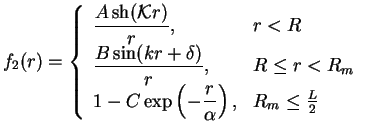 |
|
|
(2.73) |
The description of a continuous matching at the point 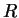 is described in
Sec. 1.3.2.3. Now we shall discuss the matching procedure at the point
is described in
Sec. 1.3.2.3. Now we shall discuss the matching procedure at the point 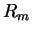 .
As usual we have three matching conditions:
.
As usual we have three matching conditions:
- Continuity of the function
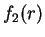 :
:
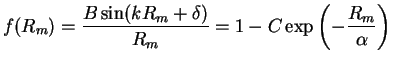 |
|
|
(2.74) |
- Continuity of the logarithmic derivative
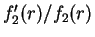 which fixes the value
of the parameter
which fixes the value
of the parameter 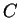 :
:
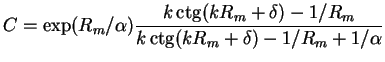 |
|
|
(2.75) |
Substitution of (2.75) into (2.74) fixes value of 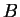
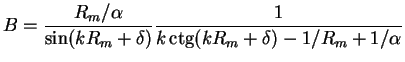 |
|
|
(2.76) |
- The kinetic energy must be continuous at
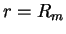 . This condition yields
. This condition yields
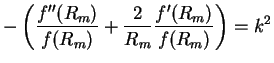 |
|
|
(2.77) |
After some mathematics the following procedure is obtained:
- By choosing the value of the scattering length
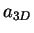 and the range of the
potential
and the range of the
potential 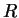 define the value of
define the value of 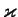 (i.e. height of the potential
(i.e. height of the potential 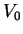 as
related by (1.54)) by solving the transcendental equation (1.59)
as
related by (1.54)) by solving the transcendental equation (1.59)
- Introduce
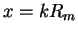 ,
,
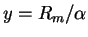 and
and
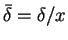 .
Both equations (1.57) and
.
Both equations (1.57) and
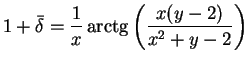 |
|
|
(2.78) |
has to be satisfied in order to loop to determine 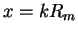 and
and 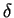 . This
can be done using iterative procedure:
. This
can be done using iterative procedure:
- Choose the value for the
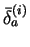 (the first time it is
initialized with
(the first time it is
initialized with
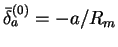 ) and obtain the value of
) and obtain the value of 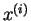 as
the solution of Eq. 2.78
as
the solution of Eq. 2.78
- Fix the scattering momentum
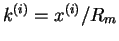 and obtain the phase
and obtain the phase
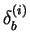 as a solution of (1.57)
as a solution of (1.57)
- Iterate
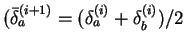 until
both numbers converge to the same value by repeating steps (a-c)
until
both numbers converge to the same value by repeating steps (a-c)
- Then the constants (A,B,C) are given by formulae
-
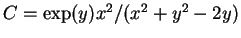
-
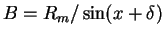
-
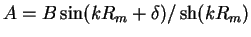
Once all parameters are fixed, the two-body term 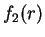 is given by (2.73),
the drift force contribution (2.39) is given by
is given by (2.73),
the drift force contribution (2.39) is given by
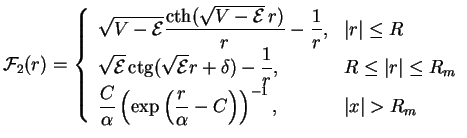 |
|
|
(2.79) |
Local energy (2.40) equals to
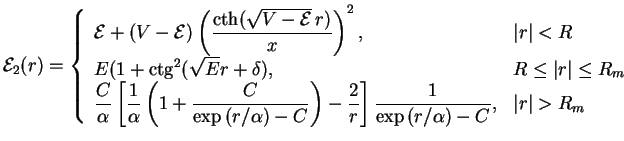 |
|
|
(2.80) |




Next: Trial wave function of
Up: Three-dimensional wave functions
Previous: Hard sphere trial wave
Contents
G.E. Astrakharchik
15-th of December 2004
![]() (1.55) is expected
to proved a good approximation for the two-body Bijl-Jastrow term
(1.55) is expected
to proved a good approximation for the two-body Bijl-Jastrow term ![]() (2.37) in a gas with the soft sphere interaction potential (1.52). At
the larger distances
(2.37) in a gas with the soft sphere interaction potential (1.52). At
the larger distances ![]() should saturate to a constant in a smooth way. We
choose an exponential type of decay:
should saturate to a constant in a smooth way. We
choose an exponential type of decay:
![]() is described in
Sec. 1.3.2.3. Now we shall discuss the matching procedure at the point
is described in
Sec. 1.3.2.3. Now we shall discuss the matching procedure at the point ![]() .
As usual we have three matching conditions:
.
As usual we have three matching conditions:
![]()
![]() is given by (2.73),
the drift force contribution (2.39) is given by
is given by (2.73),
the drift force contribution (2.39) is given by