Trial wave function of 3D zero range potential

We construct a wave function for a zero range potential in a three-dimensional case. The correct scattering length $a$ is imposed on the trial wave function $f(r)$ by corresponding boundary condition at zero distance.

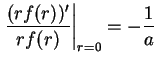$$\left.\frac{(rf(r))'}{rf(r)}\right\vert _{r=0} = - \frac{1}{a}$$ (2.81)

We choose the trial wave function in the form

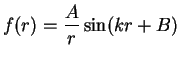$$f(r) = \frac{A}{r} \sin (kr+B)$$ (2.82)

for $r<R$ and $f(r) = 1$ otherwise.

The boundary condition at zero gives the constraint:

$$\mathop{\rm tg}\nolimits B = -ka$$ (2.83)

We impose continuity of the derivative at the matching distance which gives us another condition on the parameters of the trial wave function

$$\mathop{\rm tg}\nolimits \left(kR+B\right) = kR$$ (2.84)

The constant $B$ can be easily eliminated providing an equation which fixes the momentum $\k$:

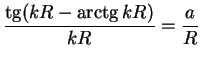$$\frac{\mathop{\rm tg}\nolimits (kR-\mathop{\rm arctg}\nolimits kR)}{kR} = \frac{a}{R}$$ (2.85)

Ones it is solved, the equation (2.83) fixes the value of the $B$. Finally the value of $A$ is fixed by continuity of the wave function itself

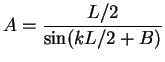$$A = \frac{L/2}{\sin(kL/2+B)}$$ (2.86)

The drift force is given by

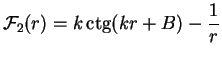$${{\cal F}_2}(r) = k\mathop{\rm ctg}\nolimits (kr+B)-\frac{1}{r}$$ (2.87)

The Bijl-Jastrow contribution to the 3D local energy depends on the distance $\r$ as

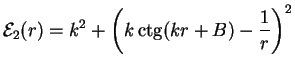$${{\cal E}_2}(r) = k^2 + \left(k\mathop{\rm ctg}\nolimits (kr+B)-\frac{1}{r}\right)^2$$ (2.88)