



Next: Conclusions
Up: Beyond Tonks-Girardeau: super-Tonks gas
Previous: One-body density matrix and
Contents
Another possible experimental signature of the super-Tonks regime can be provided by
the study of collective modes. To this aim, we calculate the frequency of the lowest
compressional mode of a system of 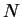 particles in a harmonic potential
particles in a harmonic potential
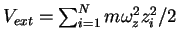 . We make use of LDA (Sec. 1.6)
which allows us to calculate the chemical potential of the inhomogeneous system
. We make use of LDA (Sec. 1.6)
which allows us to calculate the chemical potential of the inhomogeneous system
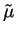 and the density profile
and the density profile 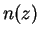 from the local equilibrium equation
from the local equilibrium equation
![$\tilde{\mu}=\mu[n(z)]+m\omega_z^2z^2/2$](img1462.gif) , and the normalization condition
, and the normalization condition
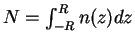 , where
, where
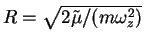 is the size of
cloud. For densities
is the size of
cloud. For densities 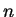 smaller than the critical density for cluster formation,
smaller than the critical density for cluster formation,
![$\mu[n]$](img1465.gif) is the equation of state of the homogeneous system derived from the fit to
the VMC energies (Fig. 6.1). From the knowledge of the density profile
is the equation of state of the homogeneous system derived from the fit to
the VMC energies (Fig. 6.1). From the knowledge of the density profile
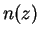 one can obtain the mean square radius of the cloud
one can obtain the mean square radius of the cloud
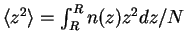 and thus, making use of the result
[MS02]
and thus, making use of the result
[MS02]
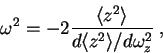 |
(6.3) |
one can calculate the frequency 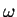 of the lowest breathing mode. Within LDA,
the result will depend only on the dimensionless parameter
of the lowest breathing mode. Within LDA,
the result will depend only on the dimensionless parameter
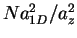 , where
, where
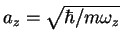 is the harmonic oscillator length. For
is the harmonic oscillator length. For 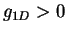 , i.e. in the case of the LL Hamiltonian, the frequency of the lowest compressional
mode increases from
, i.e. in the case of the LL Hamiltonian, the frequency of the lowest compressional
mode increases from
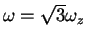 in the weak-coupling mean-field regime
(
in the weak-coupling mean-field regime
(
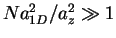 ) to
) to
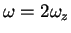 in the strong-coupling TG regime
(
in the strong-coupling TG regime
(
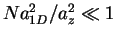 ). The results for
). The results for 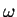 in the super-Tonks regime are
shown in Fig. 6.4 as a function of the coupling strength. In the regime
in the super-Tonks regime are
shown in Fig. 6.4 as a function of the coupling strength. In the regime
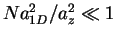 , where the HR model is appropriate, we can calculate
analytically the first correction to the frequency of a TG gas (refer to
Table 1.1).
One finds the result
, where the HR model is appropriate, we can calculate
analytically the first correction to the frequency of a TG gas (refer to
Table 1.1).
One finds the result
![$\omega=2\omega_z [1+(16\sqrt{2}/15\pi^2)(N
a_{1D}^2/a_z^2)^{1/2}+...]$](img1472.gif) . Fig. 6.4 shows that this expansion accurately
describes the frequency of the breathing mode when
. Fig. 6.4 shows that this expansion accurately
describes the frequency of the breathing mode when
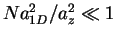 , for
larger values of the coupling strength the frequency reaches a maximum and drops to
zero at
, for
larger values of the coupling strength the frequency reaches a maximum and drops to
zero at
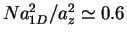 . The observation of a breathing mode with a
frequency larger than
. The observation of a breathing mode with a
frequency larger than 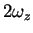 would be a clear signature of the super-Tonks
regime.
would be a clear signature of the super-Tonks
regime.
Figure 6.4:
Square of the lowest breathing mode frequency, 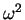 ,
as a function of the coupling strength
,
as a function of the coupling strength
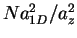 for the LL Hamiltonian
(
for the LL Hamiltonian
(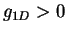 ) and in the super-Tonks regime (
) and in the super-Tonks regime (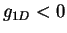 ). The dashed line is obtained
from the HR expansion (see Table 1.1).
). The dashed line is obtained
from the HR expansion (see Table 1.1).
|
|




Next: Conclusions
Up: Beyond Tonks-Girardeau: super-Tonks gas
Previous: One-body density matrix and
Contents
G.E. Astrakharchik
15-th of December 2004
![]() particles in a harmonic potential
particles in a harmonic potential
![]() . We make use of LDA (Sec. 1.6)
which allows us to calculate the chemical potential of the inhomogeneous system
. We make use of LDA (Sec. 1.6)
which allows us to calculate the chemical potential of the inhomogeneous system
![]() and the density profile
and the density profile ![]() from the local equilibrium equation
from the local equilibrium equation
![]() , and the normalization condition
, and the normalization condition
![]() , where
, where
![]() is the size of
cloud. For densities
is the size of
cloud. For densities ![]() smaller than the critical density for cluster formation,
smaller than the critical density for cluster formation,
![]() is the equation of state of the homogeneous system derived from the fit to
the VMC energies (Fig. 6.1). From the knowledge of the density profile
is the equation of state of the homogeneous system derived from the fit to
the VMC energies (Fig. 6.1). From the knowledge of the density profile
![]() one can obtain the mean square radius of the cloud
one can obtain the mean square radius of the cloud
![]() and thus, making use of the result
[MS02]
and thus, making use of the result
[MS02]
![\includegraphics[width=0.6\textwidth]{STfreq.eps}](STfreq.gif)