



Next: Collective modes
Up: Beyond Tonks-Girardeau: super-Tonks gas
Previous: Energy
Contents
Figure 6.2:
Static structure factor 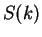 for a gas of HR at different values of the gas parameter
for a gas of HR at different values of the gas parameter 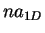 (symbols) and for a TG gas (dashed line).
(symbols) and for a TG gas (dashed line).
|
|
Contrarily to the TG case, it is not possible to obtain analytical expressions for
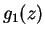 and
and 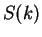 in the HR problem. We have calculated them using configurations
generated by a Monte Carlo simulation according to the exact probability
distribution function
in the HR problem. We have calculated them using configurations
generated by a Monte Carlo simulation according to the exact probability
distribution function 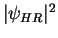 . The results for the static structure factor
are shown in Fig. 6.2. Compared to
. The results for the static structure factor
are shown in Fig. 6.2. Compared to 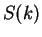 in the TG regime, a clear peak is
visible for values of
in the TG regime, a clear peak is
visible for values of 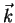 of the order of twice the Fermi wave vector
of the order of twice the Fermi wave vector 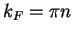 and the peak is more pronounced as
and the peak is more pronounced as 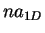 increases. The change of slope for
small values of
increases. The change of slope for
small values of 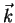 reflects the increase of the speed of sound
reflects the increase of the speed of sound 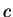 with
with 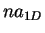 .
The long-range behavior of
.
The long-range behavior of 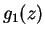 can be obtained from the hydrodynamic theory of
low-energy excitations [RC67,Sch77,Hal81]. For
can be obtained from the hydrodynamic theory of
low-energy excitations [RC67,Sch77,Hal81]. For 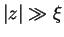 , where
, where
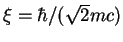 is the healing length of the system, one finds the
following power-law decay (1.199):
is the healing length of the system, one finds the
following power-law decay (1.199):
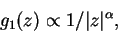 |
(6.2) |
where the exponent 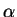 is given by
is given by
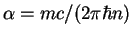 . For a TG gas
. For a TG gas
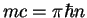 , and thus
, and thus
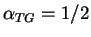 . For a HR gas one finds
. For a HR gas one finds
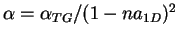 and thus
and thus
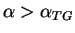 . This behavior at
long range is clearly shown in Fig. 6.3 where we compare
. This behavior at
long range is clearly shown in Fig. 6.3 where we compare 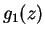 of a gas
of HR with
of a gas
of HR with 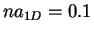 , 0.2 and 0.3 to the result of a TG gas [JMMS80]. The
long-range power-law decay of
, 0.2 and 0.3 to the result of a TG gas [JMMS80]. The
long-range power-law decay of 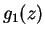 is reflected in the infrared divergence of
the momentum distribution
is reflected in the infrared divergence of
the momentum distribution
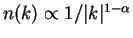 holding for
holding for 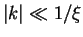 .
A gas of HR exhibits a weaker infrared divergence compared to a TG gas. The
correlation functions of a HR gas at
.
A gas of HR exhibits a weaker infrared divergence compared to a TG gas. The
correlation functions of a HR gas at 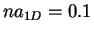 , 0.2 should accurately describe
the physical situation of a Bose gas with large and negative
, 0.2 should accurately describe
the physical situation of a Bose gas with large and negative 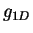 . For
. For
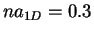 we expect already some deviations from the HR model, as it is evident
from the equation of state in Fig. 6.1, which should broaden the peak in
we expect already some deviations from the HR model, as it is evident
from the equation of state in Fig. 6.1, which should broaden the peak in
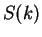 and decrease the slope of the power-law decay in
and decrease the slope of the power-law decay in 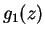 at large distances.
The analysis of correlation functions clearly shows that the super-Tonks regime
corresponds to a Luttinger liquid where short range correlations are significantly
stronger than in the TG gas.
at large distances.
The analysis of correlation functions clearly shows that the super-Tonks regime
corresponds to a Luttinger liquid where short range correlations are significantly
stronger than in the TG gas.
Figure 6.3:
One-body density matrix 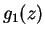 for a gas of HR at different values of the gas parameter
for a gas of HR at different values of the gas parameter 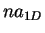 (solid lines) and for a TG gas (dashed line). Higher values of density correspond
to a faster decay of
(solid lines) and for a TG gas (dashed line). Higher values of density correspond
to a faster decay of 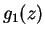 .
.
|
|




Next: Collective modes
Up: Beyond Tonks-Girardeau: super-Tonks gas
Previous: Energy
Contents
G.E. Astrakharchik
15-th of December 2004
![\includegraphics[width=0.6\textwidth]{STSk.eps}](STSk.gif)
![\includegraphics[width=0.6\textwidth]{STSk.eps}](STSk.gif)
![]() and
and ![]() in the HR problem. We have calculated them using configurations
generated by a Monte Carlo simulation according to the exact probability
distribution function
in the HR problem. We have calculated them using configurations
generated by a Monte Carlo simulation according to the exact probability
distribution function ![]() . The results for the static structure factor
are shown in Fig. 6.2. Compared to
. The results for the static structure factor
are shown in Fig. 6.2. Compared to ![]() in the TG regime, a clear peak is
visible for values of
in the TG regime, a clear peak is
visible for values of ![]() of the order of twice the Fermi wave vector
of the order of twice the Fermi wave vector ![]() and the peak is more pronounced as
and the peak is more pronounced as ![]() increases. The change of slope for
small values of
increases. The change of slope for
small values of ![]() reflects the increase of the speed of sound
reflects the increase of the speed of sound ![]() with
with ![]() .
The long-range behavior of
.
The long-range behavior of ![]() can be obtained from the hydrodynamic theory of
low-energy excitations [RC67,Sch77,Hal81]. For
can be obtained from the hydrodynamic theory of
low-energy excitations [RC67,Sch77,Hal81]. For ![]() , where
, where
![]() is the healing length of the system, one finds the
following power-law decay (1.199):
is the healing length of the system, one finds the
following power-law decay (1.199):
![\includegraphics[width=0.59\textwidth]{STg1.eps}](STg1.gif)