


Next: Lezione 22 (30 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 20 (23 maggio
Subsections
Definizione 21.1
Sia
G un grafo, un sottografo
T di
G si dirà un
albero di
copertura di
G se
- T è un albero;
- V(T)=V(G).
Osservazione 21.2
Chiaramente, se G è un grafo che possiede un albero di copertura, allora
G è connesso.
Teorema 21.3
Sia G un grafo connesso finito allora G ha un albero di copertura.
Osservazione 21.4
Il teorema precedente è vero anche senza l'ipotesi di finitezza, del grafo
G, la sua dimostrazione nel caso infinito, richiede però degli strumenti
un po' più sofisticati (il lemma di Zorn).
Alberi radicati
Definizione 21.5
Un
albero con radice è una coppia (
T,
r) con
T un albero e
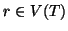
un vertice fissato che sarà detto
radice.
Se (
T,
r) e (
T',
r') sono due alberi radicati, si dirà che sono isomorfi
(come alberi radicati) se esiste un isomorfismo di grafi
f tra
T e
T' tale che
f(
r)=
r', e si scriverà
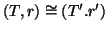
.
Esercizio 21.1
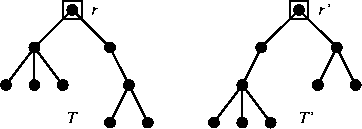
Si considerino i grafi in figura
9. Si provi che
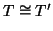
ma
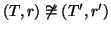
.
Figure 9:
Gli alberi radicati dell'esercizio 21.1
 |
Soluzione
La relazione 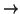 di ``paternità'' in un albero radicato
di ``paternità'' in un albero radicato
Dato un albero radicato, (T,r) per ogni vertice 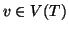 indichiamo con
Pv l'unico cammino che congiunge r con v.
indichiamo con
Pv l'unico cammino che congiunge r con v.
Proposizione 21.6
Sia (
T,
r) un albero radicato e sia
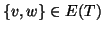
,
allora vale una e una
sola delle seguenti:
- 1.
- v è un vertice di Pw
- 2.
- w è un vertice di Pv.
Dimostrazione.
Proviamo che ne vale almeno una. Se non vale la (1), allora
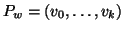 con v0=r, vk=w e
con v0=r, vk=w e 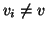 per ogni i. Ma allora,
dato che
per ogni i. Ma allora,
dato che
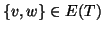 ,
,
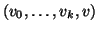 è un cammino che congiunge r
a v, per l'unicità di tale cammino
è un cammino che congiunge r
a v, per l'unicità di tale cammino
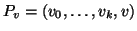 ,
e quindi vale la (2).
,
e quindi vale la (2).
Proviamo ora che non possono valere contemporaneamente. Se vale la (1), allora
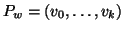 con v0=r, vk=w ed esiste un i tale che vi=v. Ma
allora
con v0=r, vk=w ed esiste un i tale che vi=v. Ma
allora
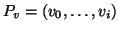 .
Dato che,
.
Dato che,
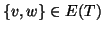 ,
,
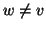 ,
quindi
i<k, e dato che Pw è un cammino
,
quindi
i<k, e dato che Pw è un cammino
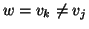 per ogni j<k, quindi w
non compare in
per ogni j<k, quindi w
non compare in
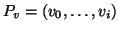 .
.

Definizione 21.7
Sia (
T,
r) un albero radicato, e siano
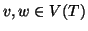
,
diremo che
v è
padre di
w, o che
w è figlio di
v, e lo indicheremo con
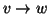
,
se
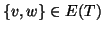
e
v è un vertice di
Pw.
Proposizione 21.8
Sia (
T,
r) un albero radicato, e sia
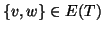
allora o
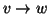
o
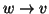
.
Inoltre per ogni
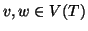
,
se
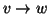
allora
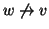
.
Dimostrazione.
È semplicemente la proposizione precedente tradotta in termini della relazione
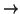 .
.

Osservazione 21.9
La proposizione
21.8 può essere interpretata dicendo che ogni
albero radicato può essere dotato in modo naturale di una struttura di
grafo diretto, in modo che ad
ogni lato dell'albero corrisponda uno ed un solo lato del grafo diretto.



Next: Lezione 22 (30 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 20 (23 maggio
Domenico Luminati
2001-06-18
![]() indichiamo con
Pv l'unico cammino che congiunge r con v.
indichiamo con
Pv l'unico cammino che congiunge r con v.
![]() con v0=r, vk=w e
con v0=r, vk=w e ![]() per ogni i. Ma allora,
dato che
per ogni i. Ma allora,
dato che
![]() ,
,
![]() è un cammino che congiunge r
a v, per l'unicità di tale cammino
è un cammino che congiunge r
a v, per l'unicità di tale cammino
![]() ,
e quindi vale la (2).
,
e quindi vale la (2).
![]() con v0=r, vk=w ed esiste un i tale che vi=v. Ma
allora
con v0=r, vk=w ed esiste un i tale che vi=v. Ma
allora
![]() .
Dato che,
.
Dato che,
![]() ,
,
![]() ,
quindi
i<k, e dato che Pw è un cammino
,
quindi
i<k, e dato che Pw è un cammino
![]() per ogni j<k, quindi w
non compare in
per ogni j<k, quindi w
non compare in
![]() .
.
![]()
![]() .
.
![]()